Как найти в0: Формулы прямолинейного равноускоренного движения

Формулы прямолинейного равноускоренного движения

☰

При прямолинейном равноускоренном движении тело

1. двигается вдоль условной прямой линии,
2. его скорость постепенно увеличивается или уменьшается,
3. за равные промежутки времени скорость меняется на равную величину.

Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с².

Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.

Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:

v = at

При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:

v = gt

Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:

a = v/t

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость).

Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с². Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

v = v₀ + at

Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:

v = v₀ – at

Получим из этих формул формулы ускорения. В случае ускорения:

at = v – v₀
a = (v – v₀)/t

В случае торможения:

at = v₀ – v
a = (v₀ – v)/t

В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:

a = v₀/t

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

t = v₀/a

Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении. Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.

При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.

Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v₀), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:

s = ½ * (v₀ + v) * t

Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v₀ + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v₀ + v₀ + at) * t = ½ * (2v₀ + at) * t = ½ * t * 2v₀ + ½ * t * at = v₀t + 1/2at²

Итак, пройденный путь определяется по формуле:

s = v₀t + at²/2

(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция. )

Если тело начало двигаться равноускоренно из состояния покоя (v₀ = 0), то формула пути упрощается до s = at²/2.

Если вектор ускорения был противоположен скорости, то произведение at

2/2 надо вычитать. Понятно, что при этом разность v₀t и at²/2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v₀/a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле:

s = v₀²/(2a)

Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи

Оглавление:

• Кинематика
• Динамика
• Статика
• Гидростатика
• Импульс
• Работа, мощность, энергия
• Молекулярная физика
• Термодинамика
• Электростатика
• Электрический ток
• Магнетизм
• Колебания
• Оптика
• Атомная и ядерная физика
• Основы специальной теории относительности (СТО)
• Равномерное движение по окружности
• Расширенная PDF версия документа «Все главные формулы по школьной физике»

 

Кинематика

К оглавлению. ..

Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:

Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v₀, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):

Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

 

Динамика

К оглавлению…

Второй закон Ньютона:

Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:

Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):

Третий закон Ньютона (сила действия равна силе противодействия):

Сила упругости:

Общий коэффициент жесткости параллельно соединённых пружин:

Общий коэффициент жесткости последовательно соединённых пружин:

Сила трения скольжения (или максимальное значение силы трения покоя):

Закон всемирного тяготения:

Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:

Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:

Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:

Скорость спутника на круговой орбите:

Первая космическая скорость:

Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:

 

Статика

К оглавлению. ..

Момент силы определяется с помощью следующей формулы:

Условие при котором тело не будет вращаться:

Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):

 

Гидростатика

К оглавлению…

Определение давления задаётся следующей формулой:

Давление, которое создает столб жидкости находится по формуле:

Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:

Идеальный гидравлический пресс:

Любой гидравлический пресс:

КПД для неидеального гидравлического пресса:

Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):

 

Импульс

К оглавлению…

Импульс тела находится по следующей формуле:

Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):

Общий импульс системы тел (важно то, что сумма векторная):

Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:

Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

 

Работа, мощность, энергия

К оглавлению…

Механическая работа рассчитывается по следующей формуле:

Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):

Мгновенная механическая мощность:

Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:

Формула для кинетической энергии:

Потенциальная энергия тела поднятого на высоту:

Потенциальная энергия растянутой (или сжатой) пружины:

Полная механическая энергия:

Связь полной механической энергии тела или системы тел и работы внешних сил:

Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):

 

Молекулярная физика

К оглавлению…

Химическое количество вещества находится по одной из формул:

Масса одной молекулы вещества может быть найдена по следующей формуле:

Связь массы, плотности и объёма:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Определение концентрации задаётся следующей формулой:

Для средней квадратичной скорости молекул имеется две формулы:

Средняя кинетическая энергия поступательного движения одной молекулы:

Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:

Следствия из основного уравнения МКТ:

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):

Газовые законы.  Закон Бойля-Мариотта:

Закон Гей-Люссака:

Закон Шарля:

Универсальный газовый закон (Клапейрона):

Давление смеси газов (закон Дальтона):

Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

 

Термодинамика

К оглавлению…

Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:

Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:

Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:

Фазовые превращения.  При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:

При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:

При сгорании топлива выделяется количество теплоты равное:

Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):

Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:

Работа идеального газа:

Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:

Изменение внутренней энергии рассчитывается по формуле:

Первый закон (первое начало) термодинамики (ЗСЭ):

Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A.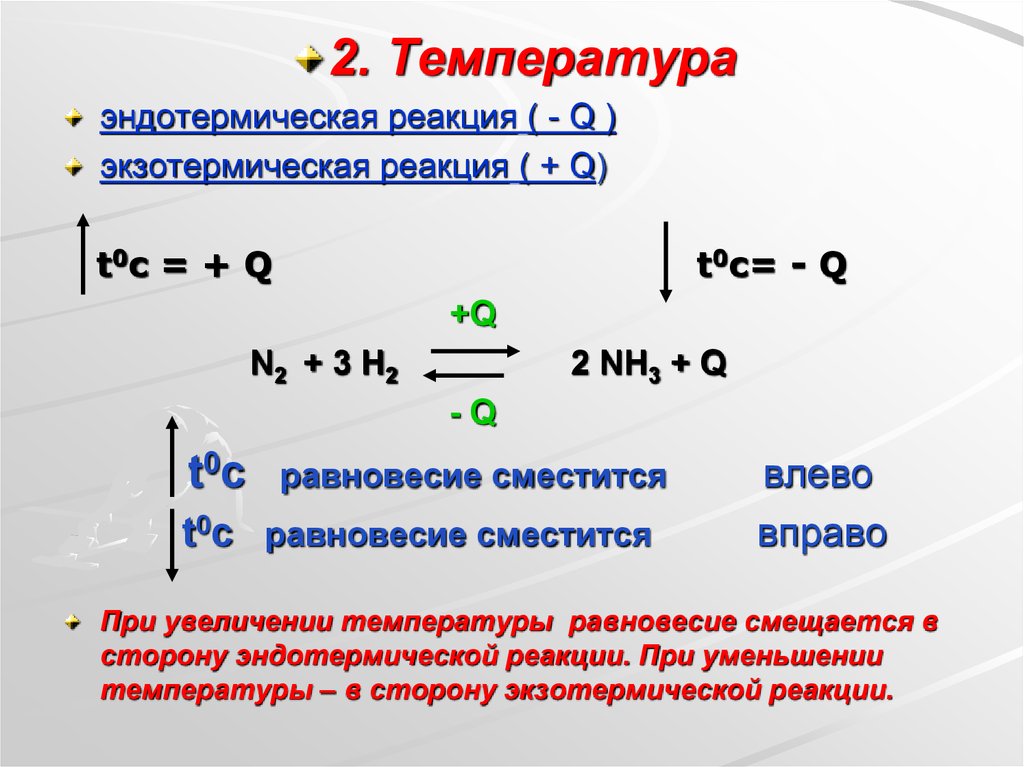 Изохорный процесс (V = const):

Изобарный процесс (p = const):

Изотермический процесс (T = const):

Адиабатный процесс (Q = 0):

КПД тепловой машины может быть рассчитан по формуле:

Где: Q₁ – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q₂ – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:

Наибольший КПД при заданных температурах нагревателя T₁ и холодильника T₂, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:

Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):

Относительная влажность воздуха может быть рассчитана по следующим формулам:

Потенциальная энергия поверхности жидкости площадью S:

Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:

Высота столба жидкости в капилляре:

При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:

При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.

 

Электростатика

К оглавлению…

Электрический заряд может быть найден по формуле:

Линейная плотность заряда:

Поверхностная плотность заряда:

Объёмная плотность заряда:

Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):

Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:

Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):

Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):

Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:

Напряженность электрического поля, которую создает заряженная плоскость:

Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:

Электрическое напряжение это просто разность потенциалов, т. е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

Определение потенциала задаётся выражением:

Потенциал, который создает точечный заряд или заряженная сфера:

Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):

Для диэлектрической проницаемости вещества верно следующее:

Определение электрической ёмкости задаётся формулой:

Ёмкость плоского конденсатора:

Заряд конденсатора:

Напряжённость электрического поля внутри плоского конденсатора:

Сила притяжения пластин плоского конденсатора:

Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):

Объёмная плотность энергии электрического поля:

 

Электрический ток

К оглавлению. ..

Сила тока может быть найдена с помощью формулы:

Плотность тока:

Сопротивление проводника:

Зависимость сопротивления проводника от температуры задаётся следующей формулой:

Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):

Закономерности последовательного соединения:

Закономерности параллельного соединения:

Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:

Закон Ома для полной цепи:

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Сила тока короткого замыкания:

Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:

Мощность электрического тока:

Энергобаланс замкнутой цепи

Полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R₁ и R₂ на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

Электролиз

Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

Где: n – валентность вещества, N_A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

 

Магнетизм

К оглавлению…

Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:

Момент сил действующих на рамку с током:

Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:

Радиус траектории полета заряженной частицы в магнитном поле:

Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:

Индукция поля в центре витка с током радиусом R:

Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:

Магнитная проницаемость вещества выражается следующим образом:

Магнитным потоком Φ через площадь S контура называют величину заданную формулой:

ЭДС индукции рассчитывается по формуле:

При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):

Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

Индуктивность катушки:

Где: n — концентрация витков на единицу длины катушки:

Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:

ЭДС самоиндукции возникающая в катушке:

Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):

Объемная плотность энергии магнитного поля:

 

Колебания

К оглавлению. ..

Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:

Период колебаний вычисляется по формуле:

Частота колебаний:

Циклическая частота колебаний:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Циклическая частота колебаний пружинного маятника:

Период колебаний пружинного маятника:

Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса:

Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:

Действующее значение напряжения:

Мощность в цепи переменного тока:

Трансформатор

Если напряжение на входе в трансформатор равно U₁, а на выходе U₂, при этом число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

Волны

Длина волны может быть рассчитана по формуле:

Разность фаз колебаний двух точек волны, расстояние между которыми l:

Скорость электромагнитной волны (в т.ч. света) в некоторой среде:

Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙10⁸ м/с, она также может быть вычислена по формуле:

Скорости электромагнитной волны (в т. ч. света) в среде и в вакууме также связаны между собой формулой:

При этом показатель преломления некоторого вещества можно рассчитать используя формулу:

 

Оптика

К оглавлению…

Оптическая длина пути определяется формулой:

Оптическая разность хода двух лучей:

Условие интерференционного максимума:

Условие интерференционного минимума:

Формула дифракционной решетки:

Закон преломления света на границе двух прозрачных сред:

Постоянную величину n₂₁ называют относительным показателем преломления второй среды относительно первой. Если n₁ > n₂, то возможно явление полного внутреннего отражения, при этом:

Формула тонкой линзы:

Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:

 

Атомная и ядерная физика

К оглавлению. ..

Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:

Импульс фотона:

Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):

Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение U_з и элементарный заряд е:

Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:

Второй постулат Бора или правило частот (ЗСЭ):

В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:

На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:

Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:

Дефект массы:

Энергия связи ядра выраженная в единицах СИ:

Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):

Формула альфа-распада:

Формула бета-распада:

Закон радиоактивного распада:

Ядерные реакции

Для произвольной ядерной реакции описывающейся формулой вида:

Выполняются следующие условия:

Энергетический выход такой ядерной реакции при этом равен:

 

Основы специальной теории относительности (СТО)

К оглавлению. ..

Релятивистское сокращение длины:

Релятивистское удлинение времени события:

Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:

Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:

Энергия покоя тела:

Любое изменение энергии тела означает изменение массы тела и наоборот:

Полная энергия тела:

Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:

Релятивистское увеличение массы:

Кинетическая энергия тела, движущегося с релятивистской скоростью:

Между полной энергией тела, энергией покоя и импульсом существует зависимость:

 

Равномерное движение по окружности

К оглавлению…

В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, a_n – центростремительное ускорение, L – длина дуги окружности, t – время):

 

Расширенная PDF версия документа «Все главные формулы по школьной физике»:

К оглавлению. ..

Как рассчитать высоту и скорость

••• master1305/iStock/GettyImages

Обновлено 08 декабря 2020 г.

Кевин Ли

Проблемы с движением снаряда часто встречаются на экзаменах по физике. Снаряд — это объект, который движется из одной точки в другую по траектории. Кто-то может подбросить предмет в воздух или запустить ракету, летящую по параболе к месту назначения. Движение снаряда можно описать с точки зрения скорости, времени и высоты. Если известны значения любых двух из этих факторов, можно определить третий.

Решите для времени

Запишите эту формулу:

v_f=v_0+at

Она утверждает, что конечная скорость, которой достигает снаряд, равна значению его начальной скорости плюс произведение ускорения под действием силы тяжести и время, когда объект находится в движении. Ускорение свободного падения является универсальной константой. Его значение составляет примерно 32 фута (9,8 метра) в секунду. Это описывает, насколько быстро объект ускоряется в секунду, если его уронить с высоты в вакууме. «Время» — это количество времени, в течение которого снаряд находится в полете.

В уравнении v _f , v ₀ и t обозначают конечную скорость, начальную скорость и время. Буква «а» является сокращением от «ускорение за счет силы тяжести». Сокращение длинных терминов облегчает работу с этими уравнениями.

Решите это уравнение относительно t, выделив его на одной стороне уравнения, показанного на предыдущем шаге. Полученное уравнение выглядит следующим образом:

t=\frac{v_f-v_0}{a}

Поскольку вертикальная скорость равна нулю, когда снаряд достигает максимальной высоты (объект, брошенный вверх, всегда достигает нулевой скорости на пике траектории), значение vf равно нулю.

Замените vf на ноль, чтобы получить следующее упрощенное уравнение:

t=\frac{0-v_0}{a}=\frac{v_0}{a}

Это означает, что когда вы бросаете или стреляете снарядом прямо в воздуха, вы можете определить, сколько времени потребуется снаряду, чтобы достичь максимальной высоты, если вы знаете его начальную скорость (v ₀ ).

Решите это уравнение, предполагая, что начальная скорость, или v ₀ , равна 10 футам в секунду, как показано ниже:

t=\frac{10}{a} 92

Решите уравнение для h. Значение составляет 1603 фута. Снаряд, брошенный с начальной скоростью 10 футов в секунду, достигает высоты 1603 фута за 0,31 секунды.

• Вы можете использовать эти же формулы для расчета начальной скорости снаряда, если знаете высоту, которую он достигает при подбрасывании в воздух, и количество секунд, которое требуется для достижения этой высоты. Просто подставьте эти известные значения в уравнения и найдите v ₀ вместо h.

Статьи по теме

Ссылки

• «Элементарный учебник физики: волновое движение»; Роберт Уоллес Стюарт; 1910
• Zoma Land Образование: движение снаряда, общее решение

Ресурсы

• Класс физики: Темы в классе физики

Советы

• Если вы знаете начальную скорость снаряда, вы можете использовать эти же формулы для расчета начальной скорости снаряда. высота, которой он достигает при подбрасывании в воздух, и количество секунд, которое требуется для достижения этой высоты. Просто подставьте эти известные значения в уравнения и найдите v0 вместо h.

Об авторе

После изучения физики Кевин Ли начал профессионально писать в 1989 году, когда в качестве разработчика программного обеспечения он также писал технические статьи для Космического центра Джонсона. Сегодня этот городской техасский ковбой продолжает выпускать высококачественное программное обеспечение, а также нетехнические статьи, охватывающие множество разнообразных тем, от игр до текущих событий.

напряжение — Как рассчитать Vo в этой схеме?

спросил 8 лет, 5 месяцев назад

Изменено 5 лет, 3 месяца назад

Просмотрено 33 тысячи раз

\$\начало группы\$

В этой схеме:

Диод идеальный диод

Диод горит т. к. V(анод) > V(катод) и тогда заменяем его на короткое замыкание.

Теперь, как рассчитать Vo, когда существуют два источника?

I = (10 + 2) / (2k + 4,7k) = 1,79 мА.

Я пытался использовать KVL:

-10 + 2k (1,79 мА) + Vo — (-2) = 0

=> Vo = 4,42

Или:

Vo = 470190 мА 470119 мА = 8,413

Какой ответ правильный? а почему другой не правильный?

• напряжение
• диоды

\$\конечная группа\$

1

\$\начало группы\$

Ни один из ответов не является правильным, но в целом у вас была правильная идея.

Вы правильно рассчитали ток во всей цепи: \$\dfrac{10 — (-2)}{2000 + 4700} = 1,791 мА\$

Следующим шагом, который вы могли бы предпринять, было бы вычислить падение напряжения на каждый резистор:

• Через резистор 2K: 2000 * 0,001791 = 3,58 В
• Через резистор 4,7К: 4700 * 0,001791 = 8,42 В

Чтобы найти напряжение на Vo, начните с любого конца и добавьте или вычтите падение напряжения на резисторе.

• Если мы начнем с конца 10 В: Vo = 10 — 3,58 = 6,42 В
• Если мы начнем с конца -2 В: Vo = -2 + 8,42 = 6,42 В

\$\конечная группа\$

1

\$\начало группы\$

Вы не «игнорируете» другие источники для использования суперпозиции, вы соединяете их с землей.

Таким образом, напряжение от источника 10 В равно 10 В * (4,7/(4,7+2)), а напряжение от источника -2 В равно -2 * (2/(4,7+2)).

Вы также можете использовать быстрый и общий метод, который работает для любого количества резисторов и соответствующих источников:

Vo = (V1/R1 + V2/R1 + … Vn/Rn) * (R1 || R2 || … ||Рн)

Где || представляет собой параллельное сопротивление 1/(1/R1 + 1/R2 + … + 1/Rn)

Таким образом, в этом случае Vo = (10/2 — 2/4,7)(4,7 || 2)

Либо метод должен дать тот же результат, если вы не сделаете ошибок.

\$\конечная группа\$

\$\начало группы\$

Диод идеальный и смещен в прямом направлении, поэтому происходит короткое замыкание.

Ток в резисторах равен \$\dfrac{12V}{4k7+2k0}\$ = 1,791 мА (что вы уже подсчитали)

Напряжение на 4k7 составляет 1,791 мА * 4k7 = 8,418 вольт.

Но нижняя часть резистора 4k7 на 2 вольта ниже, поэтому выходное напряжение составляет 6,418 вольт.

Ни один из ваших ответов неверен.

\$\конечная группа\$

2

\$\начало группы\$

Первая задача — определить, смещен ли диод в прямом или обратном направлении. Вы можете думать об этом так, представьте, что диод смещен в обратном направлении, в этом случае анод получает 10 В, а катод получает -2, что означает, что ваше предположение об обратном смещении диода неверно, и он должен быть смещен в прямом направлении.

Теперь, когда мы знаем, что диод проводит ток, применим простое узловое уравнение в точке выхода:

(Vo-10)/2k + (Vo+2)/4,7k =0;

Решите для Vo, которое будет примерно 6,42 В.

\$\конечная группа\$

\$\начало группы\$

Поскольку в цепи имеется более одного источника напряжения, почему бы не использовать теорему о суперпозиции (http://en.wikipedia.org/wiki/Superposition_theorem). Поместите источник -2 В в ноль и примените правило делителя напряжения, чтобы найти: Vo (-2 В с заземлением) = 10 В x 4,7 кОм/(4,7 кОм + 2 кОм) = 7,0 В. Затем поместите источник +10 В в ноль и примените правило делителя напряжения, чтобы найти Vo(+10В заземление) = -2В x 2к/(4,7к+2К) = -0,6В. Суммируйте эти два результата, чтобы получить фактический Vo: Vo = Vo (-2 В с заземлением) + Vo (+10 В с заземлением) = 7,0–0,6 = 6,4 В Вам нужно использовать только 2 цифры точности, потому что это все, с чего вам нужно начать в данных вашей схемы.