Лестница онлайн расчет: Онлайн расчёт прямой лестницы на тетивах

Содержание

Расчет металлической лестницы онлайн — чертеж

В этом разделе можно спроектировать металлическую лестницу. Вы получите проект лестницы и 3D модель внешнего вида лестницы в масштабе.
Вам не придётся «выдумывать велосипед» все возможные конструкции лестниц уже есть в наборе, вам нужно просто подставить свои размеры исходя из ваших условий. Расчет металлической лестницы онлайн — это просто.

Сначала выберете подходящий вам тип конструкции лестницы, потом введите ваши размеры и нажмите рассчитать, получите ваш индивидуальный чертеж металлической лестницы и проект лестницы в 3D.





Сегодня металлические лестницы могут похвастаться большой популярностью и высоким спросом, поскольку характеризуются отличной прочностью, надежностью, долговечностью. Лестницы на металлической основе, при желании, могут быть дополнены различными видами отделочного материала — деревом, стеклом, искусственным либо натуральным камнем, плиткой.

Преимущества:

— прочность. Металлическая конструкция способна выдерживать значительные нагрузки и механические воздействия;
— долговечность. Лестницы из металла устойчивы к влиянию влаги, температурных колебаний, солнечного света;
— ассортимент. Существует несколько методик производства и обработки лестничных маршей, благодаря чему изделию можно придать различную конфигурацию и внешний вид;
— универсальность. Металлические лестницы активно используются для установки в частных домах, муниципальных учреждениях, производственных помещениях;
— простота монтажа. К наиболее распространенному виду относятся сборные конструкции, так как их установка занимает минимум времени и не требует больших усилий.

Особенности изделий

В качестве производственного материала может выступать железо, сталь, алюминий, чугун. В целях обеспечения надежной защиты готовая продукция покрывается порошковым красящим веществом, полимерами, хромом.

Металлическая конструкция может быть:
— сварной. Обычно для изготовления применяется нержавейка. Все комплектующие производятся с учетом заранее
подготовленных чертежей, прочно фиксируются между собой на месте установки;
— сборной. Сооружение включает в себя несколько отдельных элементов в виде перил, опор, ограждений, крепежных деталей. Сборка осуществляется также на месте монтажа;
— литой. Считается наиболее затратным методом производства лестничного марша. Для изготовления используется латунь, бронза;
— кованой. Всем составляющим конструкции присуще сложная форма, лестница отличается изысканным видом, высокой декоративностью.

Принципы выбора

При изготовлении лестницы на заказ следует учитывать ряд важных факторов:
— металлическое сооружение должно быть дополнительно обработано антикоррозионным специальным составом;

— лестница, в первую очередь, должна быть удобной и безопасной. При изготовлении должен учитываться размер ступеней, расстояние между ними, наклон марша;
— для обеспечения максимальной надежности, рекомендуется заказывать металлическую лестницу с перилами.

Благодаря широкому модельному ряду продукции, сегодня лестницы из металла могут прекрасно вписаться в любой интерьер помещения с учетом конкретно выбранного стиля.

Расчет винтовой лестницы. Онлайн-калькулятор, чертежи, расчеты

Содержание

  • 1 Типы спиральных лестниц эконом-класса
  • 2 Расчет спиральных лестниц
  • 3 Расчет винтовой лестницы онлайн
  • 4 Винтовая лестница: чертеж

В настоящее время все больше людей придерживаются минимализма в интерьере и стиле. При строительстве такой подход не исключение.

При желании создать удобную и функциональную лестницу при минимальных затратах советуем вам рассмотреть эконом-вариант спиральной конструкции. Для того чтобы исключить лишние затраты на материалы и трудозатраты, важно правильно произвести расчет винтовой лестницы.

Типы спиральных лестниц эконом-класса

При выборе эконом-варианта мы сталкиваемся с двумя критериями, определяющими стоимость.

Первый критерием является материал изготовления, это может быть дерево, металл, бетон. Исходя из стоимости материала, оптимальным решением будет использовать дерево.

Вторым критерием является вариант конструкции, их также несколько:

  • на косоуре.

  • На тетиве.

  • Консольная.

  • На больцах.

В результате рассмотрения представленных вариантов можно смело сделать вывод, что оптимальное решение винтовой лестницы на второй этаж эконом-класса — это деревянная, на больцах.

Расчет спиральных лестниц

Расчет винтовой лестницы необходим для создания проекта и точного понимания объемов предстоящих работ.

Расчет винтовой лестницы рассмотрим на примере конструкции с полным кругом вращения 360° и высотой этажа 300 см. Ширину марша возьмем 100 см, с центральной опорой 20 см, общий диаметр всей конструкции составляет 220см.

  • Начнем с определения длины окружности по внешнему краю и по траектории движения. Воспользуемся формулой L=πd, для внешней длины получаем Lв=3,14*220=690,8 см. Траектория движения определена из расчета 2/3 от радиуса строения, в результате получаем Lд=3,14*220*2/3=460,5 см.
  • Опираясь на оптимальные значения размеров ступеней, определим их количество и размер. Рассмотрим вариант использования 17 шт., в таком случае высота каждой составит 300/17=18 см. Если высота получается дробной, допускается увеличить первую ступень с целью обеспечить одинаковый размер на все остальные. Ширина проступи по траектории движения составит 460,5/16=29 см (17-я ступень — это уже площадка второго этажа).
  • Исходя из полученных данных, проверяем по формуле 2*а+с=60-65 см соответствие размеров стандарту ширины шага 2*18+29=65.
  • Аналогично определим ширину проступи по внешнему краю 690,8/16=43 см.
  • В точке крепления к опорному столбу ширина проступи определяется из расчета утроенного диаметра несущего столба, на который они нанизываются. Возьмем для примера диаметр столба 50 мм, в таком случае ширина в точке крепления составляет 150 мм.
  • Промежуточные бочонки, которыми чередуются проступи, соответственно будут иметь размеры: внутренний диаметр — равный диаметру столба, внешний – ширине ступени в точке крепления, а высота будет равняться высоте ступени.

Расчет винтовой лестницы онлайн

Рассчитать винтовую лестницу онлайн можно, воспользовавшись онлайн-калькулятором.

Винтовая лестница: чертеж

Перед тем как приступить к закупке материалов и монтажу, рекомендуем сделать чертеж будущего строения.

Выполнив чертеж, вы убедитесь в том, что расчет винтовой лестницы выполнен правильно. Если на этапе создания чертежа вы заметите какие-либо не стыковки в параметрах, вы сможете их исправить без лишних затрат.

Создать чертеж мы рекомендуем при помощи специальных программ (AutoCad или Solidworks), это позволит вам без лишних проблем вносить изменения на этапе проектирования.

Поделиться с друзьями:

Твитнуть

Поделиться

Поделиться

Отправить

Класснуть

Adblock
detector

Лестница на стене • pickshares

Начало » Упражнения » Инженерная механика I » Лестница на стене

В этом упражнении показано решение упражнения по классической механике «лестница на стене» и рассматриваются следующие вопросы:

  • Какие силы действуют на лестница, прислоненная к стене?
  • Когда лестница скользит?

Внизу страницы находится онлайн-калькулятор для проверки различных комбинаций коэффициентов статического трения, длин и углов.

Задание

Лестница прислонена к стене. На полу и на стене разные материалы, поэтому значения статического трения различаются. На какую высоту (расстояние l) может подняться по лестнице человек с весом G, не поскользнувшись?

Лестница на стене

Решение

Чтобы решить задачу, лестница срезается на первом шаге. Система координат установлена ​​на x-y, а моменты поворота влево положительны.

Диаграмма свободного тела для лестницы на стене

Затем отмечают баланс сил в направлениях x и y и баланс моментов вокруг B.

\[ \require{отменить} \]

Баланс сил в направлении x равен

\[ \tag{1} \sum F_x = 0 = F_{Ax} — F_{Bx} \]

Баланс сил в направлении y равен

\[ \tag{2} \sum F_y = 0 = F_{Ay} + F_{By} — G \]

Баланс моментов вокруг B равен

\[ \tag{3} \sum M( Б) = 0 = G \cdot l \cdot \cos \alpha — F_{Ay} \cdot L \cdot \cos \alpha — F_{Ax} \cdot L \cdot \sin \alpha \]

силы F Ay и F Bx зависят от своих нормальных сил и коэффициентов статического трения.

\[ \require{отменить} \]

\[ \tag{4} F_{Ay} = F_{Ax} \cdot µ_A \]

\[ \tag{5} F_{Bx} = F_{By} \cdot µ_B \]

Уравнение ( 1) решается для F Ax и F Bx из уравнения (5) вставляется:

\[ \require{отменить} \]

\[ \tag{6} F_{Ax} = F_{By} \cdot µ_B \]

Полученный результат подставляется непосредственно в уравнение (4).

\[ \tag{7} F_{Ay} = F_{By} \cdot µ_A \cdot µ_B \]

F Ay используется в балансе сил в направлении y, уравнение (2), и уравнение решается для F By :

\[ \require{отменить} \]

\[ \tag{8} 0 = F_{By} + F_{By} \cdot µ_A \cdot µ_B — G \]

\[ \tag{9} F_{By} = \frac{G} {µ_A \cdot µ_B + 1} \]

Это означает, что теперь также можно вычислить F Ax и F Ay .

\[ \tag{10} F_{Ax} = \frac{G \cdot µ_A}{µ_A \cdot µ_B + 1} \]

\[ \tag{11} F_{Ay} = \frac{G \cdot µ_A \cdot µ_B}{µ_A \cdot µ_B + 1} \]

Баланс моментов (3) преобразуется в соответствии с длиной l и используются расчетные значения.

\[ \require{отменить} \]

\[ \tag{12} l=\frac{{F_{\mathit{Ax}}} \cdot L \cdot \sin{\left(\alpha \right)}+{F_{\mathit{Ay} }} \cdot L \cdot \cos{\left(\alpha \right) }}{G \cdot \cos{\left(\alpha \right) }} \]

\[ \tag{13} l= \ frac {\ frac {G \ cdot L \ cdot {µ_B} \ cdot \ sin {\ left ( \ alpha \ right)}} {{µ_A} \ cdot {µ_B} +1} + \ frac {G \ cdot L \cdot {µ_A} \cdot {µ_B} \cdot \cos{\left(\alpha \right)}}{{µ_A} \cdot {µ_B}+1}}{G \cdot \cos{\left(\alpha \справа) }}\]

или укороченный и измененный:

\[ \tag{14} l=\frac{L \cdot {µ_B} \cdot \sin{\left(\alpha \right) }+L \cdot {µ_A} \cdot {µ_B} \cdot \cos{\left(\alpha \right)}}{\left( {µ_A} \cdot {µ_B}+1\right) \cdot \cos{\left(\alpha \right)}} \]

Искомая длина определена. Как и ожидалось, сила веса может быть уменьшена для расчета, так что это не повлияет на результат.

Онлайн-калькулятор

Результат можно проверить здесь.

Если вы введете значения, то обнаружите, что функция вычисляет длину для угла 0° (или если вы оставите поле пустым) или для очень малых углов.

Что это значит?

На первый взгляд это может показаться неправильным, но это правильно. Расчетная длина находится ниже центра тяжести лестницы до определенного угла. Любой вес, действующий на лестницу выше этой длины, приведет к соскальзыванию лестницы. А из-за центра тяжести посередине лестницы так и бывает до определенного угла. В качестве примера: лестница с коэффициентом статического трения 0,5 как в A, так и в B будет стоять отдельно только под углом прибл. 37°.

А теперь попробуйте сами:

Длина L в м

Коэффициент трения покоя μ A

Коэффициент трения покоя μ B

Угол α в ° еще много интересных упражнений

3 90 относительно статики здесь.

Гипотенуза треугольника. Калькулятор

Автор: Hanna Pamuła, PhD

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 20 ноября 2022 г.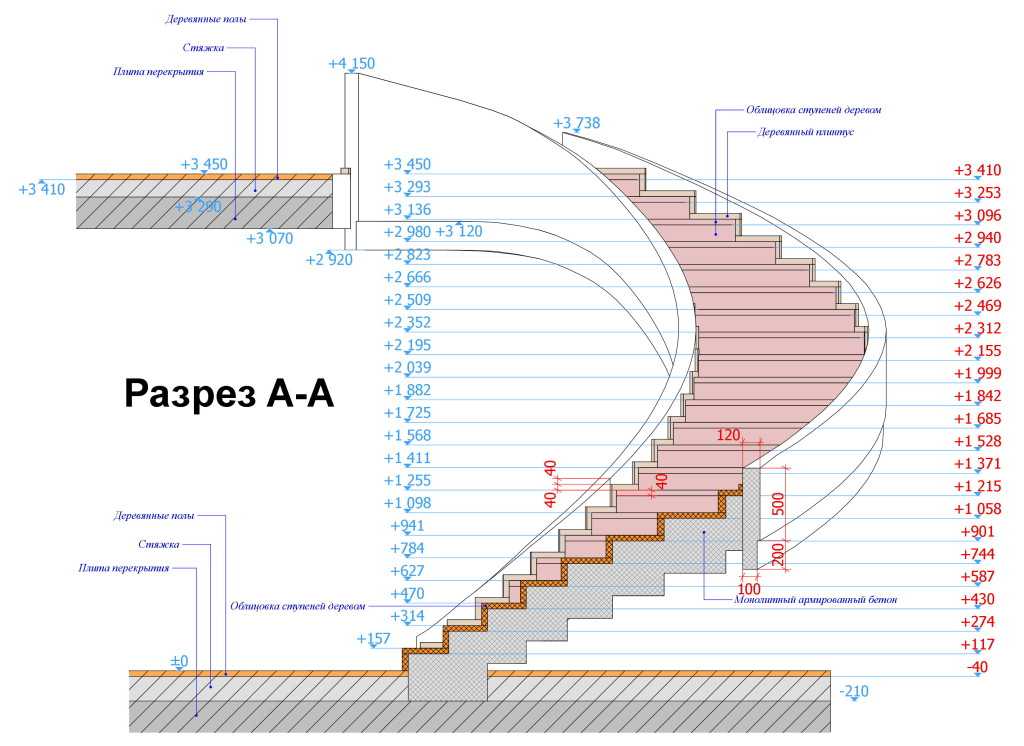

Содержание:
  • Что такое гипотенуза треугольника
  • Формула гипотенузы треугольника
  • Как найти гипотенузу прямоугольного треугольника с помощью этого калькулятора гипотенузы?
  • Часто задаваемые вопросы

С помощью этого калькулятора гипотенузы вы быстро найдете самую длинную сторону прямоугольного треугольника. Если вы хотите узнать, что такое гипотенуза прямоугольного треугольника, как ее найти и что такое гипотенуза в формуле треугольника, вы найдете ответ ниже с простым примером, чтобы все прояснить. Не ждите больше; попробуйте этот калькулятор гипотенузы!

Что такое гипотенуза треугольника

Гипотенуза — это самая длинная сторона прямоугольного треугольника . Это сторона, противоположная прямому углу (90°). Длину гипотенузы можно найти, например, из теоремы Пифагора. Вы можете узнать больше об этом в нашем калькуляторе теоремы Пифагора.

Формула гипотенузы треугольника

В этом калькуляторе гипотенузы реализовано несколько формул — таким образом, мы убедились, что он подходит для различных сценариев, с которыми вы можете столкнуться.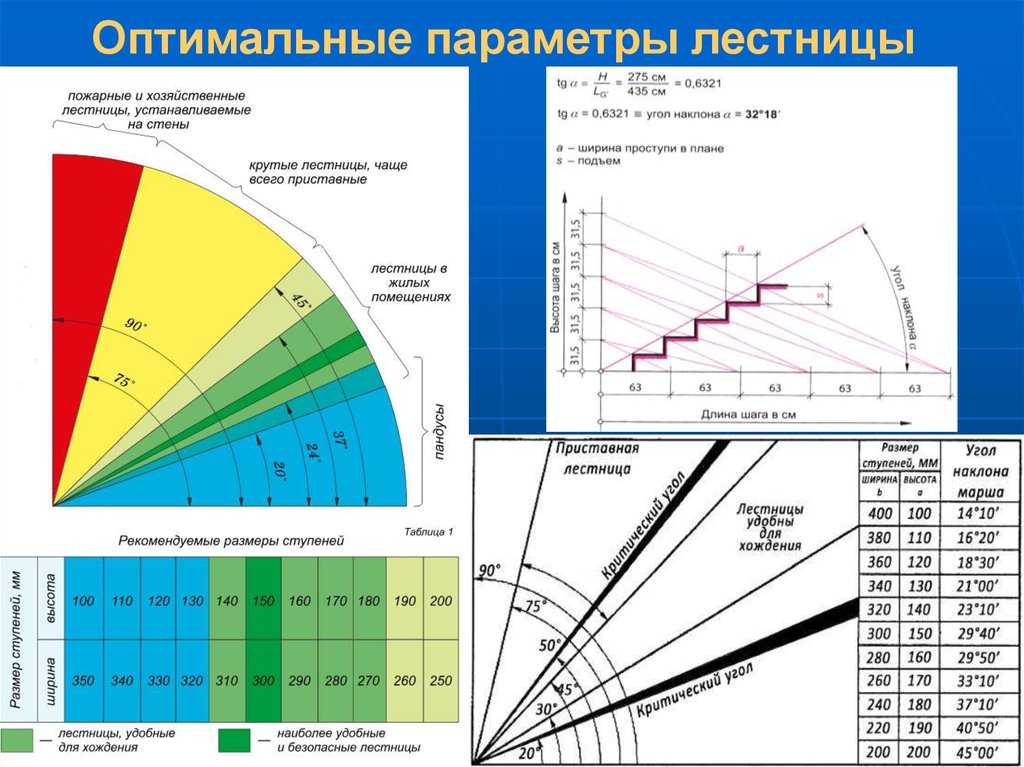

Вы можете найти гипотенузу:

  1. Даны две стороны прямоугольного треугольника

Используйте теорему Пифагора для вычисления гипотенузы по сторонам прямоугольного треугольника. Извлеките квадратный корень из суммы квадратов:

  • c = √(a² + b²)
  1. Дан угол и одна сторона
  • c = a / sin(α) = b / sin(β) , объясняется в нашем калькуляторе закона синусов.
  1. Учитывая площадь и одну ветвь

Так как площадь прямоугольного треугольника равна a × b / 2 , то

  • c = √(a² + b²) = √(a² + (площадь × 2 / a)²) = √( (площадь × 2 / b)² + b²)
    .

Чтобы узнать больше о вычислениях с прямоугольными треугольниками, посетите нашу область калькулятора прямоугольного треугольника и калькулятора сторон и углов прямоугольного треугольника.

Как найти гипотенузу прямоугольного треугольника с помощью этого калькулятора гипотенузы?

Давайте посчитаем, какой длины должна быть лестница, если мы хотим спасти котенка с 10-футовой крыши. Калькулятор помогает найти длину лестницы от земли до края крыши, но не забывайте о той части лестницы, которая должна выходить за край!

  1. Выберите вариант, необходимый для ваших расчетов . Мы знаем, что наша крыша имеет высоту 10 футов и что самый безопасный угол для лестницы составляет ~75,5°. Из выпадающего списка данного поля выберите опцию: угол ∡ и одна сторона .
  2. Изменить единицы измерения на футы .

  1. Введите указанные значения

    . Наша нога a имеет длину 10 футов, а угол α между лестницей и землей равен 75,5°.

  2. Длина лестницы, гипотенуза прямоугольного треугольника , появляется! Равен 10,33 фута.

    Также отображаются угол β = 14,5° и катет b = 2,586 фута. Вторая ножка также является важным параметром, так как она говорит вам, как далеко вы должны разместить лестницу от стены (точнее, от края крыши). Общий принцип, который следует помнить, — это правило 4:1 : на каждые четыре фута высоты по вертикали ножка лестницы должна отодвигаться от стены на один фут.

Часто задаваемые вопросы

Как найти гипотенузу с грехом?

  1. Выполнить операцию sin над углом (не прямым углом).
  2. Разделить длину стороны , противоположной углу, использованному в шаге 1, на результат шага 1.
  3. Результатом является гипотенуза .

Всегда ли гипотенуза является самой длинной стороной?

Да, гипотенуза всегда самая длинная сторона , но только для прямоугольных треугольников. В равнобедренных треугольниках две равные стороны называются катетами, а в равнобедренном треугольнике все стороны называются просто сторонами.

Как найти смежную и противоположную гипотенузу?

  1. Найдите самую длинную сторону и назовите ее гипотенузой .
  2. Вы можете найти смежную и противоположную стороны, только если выберете один угол меньше 90 градусов.
  3. Прилегающая сторона — это сторона, которая вместе с гипотенузой образует выбранный угол .
  4. Противоположная сторона — это сторона, которая не образует выбранный угол .

Как найти высоту гипотенузы?

  1. Нарисуйте высоту гипотенузы треугольника. Два новых треугольника, которые вы создали, подобны друг другу и основному треугольнику.
  2. Разделите длину самой короткой стороны главного треугольника на гипотенузу главного треугольника.
  3. Умножьте результат на длину оставшейся стороны, чтобы получить длину высоты.
  4. В качестве альтернативы, углы внутри меньших треугольников будут такими же, как углы основного треугольника, так что вы можете выполнить тригонометрию , чтобы найти его другим способом.

Что делать, если гипотенуза противоположна?

Если гипотенуза противоположна, то вы считаете неправильный угол — вы не можете использовать тригонометрию с прямым углом треугольника. Рассмотрим один из других углов. Это как смежный угол. Противоположная сторона будет той стороной, которая не образует этот угол.

Как построить прямую, перпендикулярную гипотенузе?

  1. Приобретите циркуль, линейку и ручку или карандаш.
  2. Установите циркуль на длину гипотенузы (или любую длину, если она остается постоянной).
  3. Нарисуйте окружность с центром на одном из концов гипотенузы.
  4. Нарисуйте еще один круг с центром на другом конце гипотенузы.
  5. Нарисуйте линию, соединяющую две точки , где пересекаются эти окружности. Эта линия перпендикулярна гипотенузе.

Как найти гипотенузу равнобедренного прямоугольного треугольника?

  1. Найдите длину одной из не гипотенузных сторон .
  2. Квадрат по длине стороны.
  3. Удвоить результат предыдущего шага.
  4. Квадратный корень результат шага 3.
РубрикаРазное