Онлайн калькулятор доски в кубах: Калькулятор доски для точного расчета количества материала

Содержание

Калькулятор расчета количества досок для опалубки ленточного фундамента

Для заливки фундаментной ленты бетоном необходимо соорудить надежную опалубку, которая будет способна выдержать немалое давление тяжелого полужидкого раствора до его схватывания, придать конструкции чёткую задуманную форму. В наше время существует немало интересных способов сборки опалубки, но все же в большинстве случаев при индивидуальном «малом» строительстве хозяева предпочитают «классику» – щиты из досок.

Калькулятор расчета количества досок для опалубки ленточного фундамента

Вполне понятным становится вопрос – а сколько же досок потребуется для сколачивания этих щитов? Ответ на него поможет получить калькулятор расчета количества досок для опалубки ленточного фундамента.

Некоторые пояснения и дополнительные справочные данные – в текстовом блоке под калькулятором.

Цены на доску обрезную

~~доска обрезная~~

Калькулятор расчета количества досок для опалубки ленточного фундамента

Перейти к расчётам

Введите запрашиваемые значения и нажмите «Рассчитать количество досок»

Суммарная длина ленты фундамента

Толщина ленты фундамента

Необходимая высота опалубки

Рассчитать для доски шириной:

100 мм 125 мм 150 мм

Пояснения по проведению расчета

Сам расчет – несложен, и базируется на известных геометрических размерах будущей фундаментной ленты. Так, необходимо будет указать:

Длину фундаментной ленты: с учетом периметра здания и всех внутренних перемычек – оснований под капитальные перегородки, если они предусмотрены конструкцией.
Толщину фундаментной ленты.
Высоту опалубки. Вот здесь могут возникнуть разночтения. Нередко опалубку монтируют только для цокольной части фундамента, а ниже уровня поверхности грунта роль опалубки уже выполняют тщательно выровненные стенки выкопанных траншей (как показано на иллюстрации ниже):

Один из вариантов – опалубка ставится только на цокольной части фундамента.

Такой подход хорош для малозаглубленных лент – позволяет достичь определенной экономии материалов. Однако, если требуется мощный фундамент, с залеганием ниже уровня промерзания грунта, то его, после полного застывания и набора прочности бетоном, рекомендуется тщательно гидроизолировать и утеплить. В таких случаях опалубку, как правило, делают на всю высоту ленты – от ее подошвы и до верхнего торца цоколя.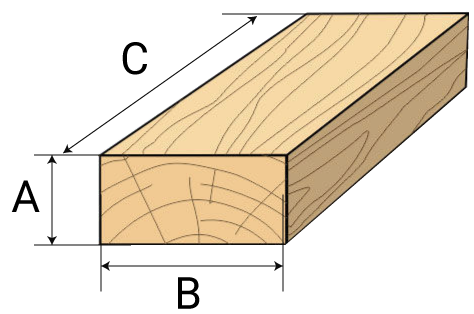

Опалубка смонтирована на всю высоту фундаментной ленты

Таким образом, в это поле калькулятора должна вноситься именно высота опалубки, в зависимости от выбранного варианта из упомянутых выше.

Необходимо выбрать ширину приобретаемой доски из трех вариантов – 100, 125 и 150 мм.

Толщина доски в данном расчете непринципиальна, но определиться с ней стоит заранее, так как это напрямую будет влиять на общую стоимость приобретаемого объема древесины. И толщина – дело отнюдь не произвольное: есть специальные нормы, которые рассчитаны для того, чтобы доски гарантированы выдержали нагрузку от бетонного раствора, не ломаясь и не прогибаясь.

Толщина доски зависит от высоты опалубки и шага установки вертикальных стоек

Доски сколачиваются в щиты с использованием вертикальных стоек, которые, в свою очередь, при монтаже опалубки подпираются дополнительными кольями, распорками, и т.п. Толщина используемых досок для щитов зависит от высоты опалубки и расстояния между этими вертикальными стойками. Для правильного выбора можно воспользоваться следующей таблицей.

Планируемая высота стенок опалубки, м	Шаг установки вертикальных стоек опалубки, м
	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
0.2	19	19	19	25	25	25	40	40
0.3	19	19	19	25	25	40	40	40
0.4	19	19	22	25	40	40	40	40
0.5	19	19	22	25	40	40	40	50
0.6	19	19	25	40	40	40	40	50
0. 7	19	22	25	40	40	40	40	50
0.8	19	22	40	40	40	50	40	60
0.9	19	22	40	40	40	50	40	60
1	19	25	40	40	40	50	40	60
1.1	19	25	40	40	40	50	50	60
1.2	19	25	40	40	50	50	50	60
1.3	19	25	40	40	50	50	50	60
1.4	19	40	40	40	50	50	50	60
1.5	22	40	40	40	50	60	50	60
1.6	22	40	40	50	50	60	60	60
1. 7	22	40	40	50	50	60	60	60
1.8	22	40	40	50	50	60	60	60
1.9	22	40	40	50	50	60	60	75
2	25	40	40	50	50	60	75	75

Естественно, что при выборе конкретных параметров (толщины и ширины) приобретаемых досок, нужно проявлять действительно хозяйственный подход. Раз заливается фундамент, то, надо полагать, впереди предстоит еще очень много строительных работ. И доски после распалубки и разборки щитов должны найти должное применение – они не теряют своих качеств и могут использоваться как полноценный строительный материал. Например, ничто не должно помешать применить их в конструкции перекрытий, стропильной системы, стен в подсобных постройках и т.п.

Как собирается опалубка для фундамента?
Современные технологии строительства предлагают немало интересных подходов к решению этой проблемы. Подробнее о монтаже опалубки для заливки фундамента – в специальной публикации нашего портала.

Понравилась статья?
Сохраните, чтобы не потерять!

Оцените:

3.6

Калькулятор расчета объема груза — Avrora Logistic

На главную
Расписание

движения
КАЛЬКУЛЯТОР
ТАМОЖЕННЫХ
ПЛАТЕЖЕЙ
КАЛЬКУЛЯТОР
СБОРНЫХ
ГРУЗОВ
КАЛЬКУЛЯТОР
ЦЕЛЫХ
КОНТЕЙНЕРОВ
РАСЧЕТ ОБЪЕМА
ГРУЗА

Рассчитайте объем вашего груза

РАСЧЕТ ОБЪЕМА ГРУЗА

ШИРИНА (W) *

ДИАМЕТР (D) *

РАСЧЕТ ОБЪЕМА КоробкиЦилиндр

ВЫСОТА (H) * ЕДИНИЦА ИЗМЕРЕНИЯ * ммсмм

ДЛИНА (L) *

КОЛИЧЕСТВО КОРОБОК *

КОЛИЧЕСТВО ЦИЛИНДРОВ *

ИТОГО:

Объем одной коробки

Объем одного цилиндра

0 м³

Общий объем

0 м³

ИСПОЛЬЗУЙТЕ ПОЛУЧЕННЫЕ РАСЧЕТЫ
ДЛЯ ОФОРМЛЕНИЯ ЗАЯВКИ

На главную

Расписание
движения
РАСЧЕТ ОБЪЕМА
ГРУЗА
КАЛЬКУЛЯТОР
ТАМОЖЕННЫХ
ПЛАТЕЖЕЙ
КАЛЬКУЛЯТОР
СБОРНЫХ
ГРУЗОВ
КАЛЬКУЛЯТОР
ЦЕЛЫХ
КОНТЕЙНЕРОВ

Возникли вопросы?

Я согласен на обработку персональных данных в порядке и на условиях, указанных по ссылке

Прикрепить файл (максимальный размер 20 Мб)

Калькулятор вероятности игры в кости

Создано Wojciech Sas, PhD

Отредактировано Bogna Szyk и Jack Bowater

Последнее обновление: 13 февраля 2023 г.

Когда использовать калькулятор вероятности игры в кости?

Играть или пасовать? — Давай сыграем в игру!

Часто задаваемые вопросы

Калькулятор вероятности броска костей — отличный инструмент, если вы хотите оценить вероятность броска кубиков по множеству вариантов . В набор входит множество различных многогранных кубиков, так что вы можете исследовать вероятность выпадения 20-гранного кубика и обычного кубического кубика.

Итак, просто оценивайте шансы и играйте! Вы также найдете краткие описания каждой опции в тексте.

🔎 У тебя нет физических кубиков? Нет проблем — попробуйте наш калькулятор игры в кости!

Многогранный кубик

Все знают, что такое обычный 6-гранный кубик, и, скорее всего, многие из вас уже сыграли тысячи игр, где использовалась одна (или более) t Но знаете ли вы, что существует разные типы штампов ? Из бесчисленных возможностей самые популярные игральные кости включены в набор игральных костей Dungeons & Dragons , который содержит семь различных многогранных игральных костей: равносторонний треугольник;

6-гранный кубик , классический куб — каждая грань представляет собой квадрат;

8-гранная игральная кость , также известная как октаэдр — каждая грань представляет собой равносторонний треугольник;

10-гранная игральная кость , также известная как пятиугольный трапецоэдр — каждая грань представляет собой воздушного змея;

12-гранный кубик , также известный как додекаэдр — каждая грань представляет собой правильный пятиугольник; и

20-гранный кубик , также известный как икосаэдр — каждая грань представляет собой равносторонний треугольник.

💡 Вы можете отточить свою стратегию D&D, используя калькулятор покупки очков Omni 5e.

Не волнуйтесь, мы учитываем каждый из этих кубиков в нашем калькуляторе вероятности. Вы можете выбрать то, что вам нравится, и, например, притвориться, что бросаете сразу пять 20-гранных кубиков!

Как рассчитать вероятность броска костей?

Что ж, вопрос сложнее, чем кажется на первый взгляд, но вскоре вы убедитесь, что ответ не так уж и страшен! Все дело в математике и статистике.

Прежде всего, мы должны определить какую вероятность броска костей мы хотим найти . Мы можем выделить несколько, которые вы можете увидеть в этом калькуляторе вероятности игры в кости.

Прежде чем приступать к каким-либо вычислениям, давайте определим некоторые переменные, которые мы будем использовать в формулах. n – количество игральных костей, s – количество отдельных граней кости, p – вероятность выпадения любого значения с кости, а P – общая вероятность решения задачи. Существует простое соотношение – p = 1/с , поэтому вероятность получить 7 на 10-гранном кубике в два раза больше, чем на 20-гранном кубике.

Вероятность выпадения одного и того же значения на каждом кубике – хотя шанс выпадения определенного значения на одном кубике равен p , нам нужно только умножить эту вероятность на саму себя столько раз, сколько игральных костей. Другими словами, вероятность P равна p в степени n , или P = pⁿ = (1/s)ⁿ . Если мы рассмотрим три 20-гранных кубика, шанс выпадения 15 на каждом из них составляет: P = (1/20)³ = 0,000125 (или P = 1,25·10⁻⁴ в экспоненциальном представлении). И если вы заинтересованы в прокатке набора из любых одинаковых значений, просто умножьте результат на общее количество граней кубика: P = 0,000125 · 20 = 0,0025 .
Вероятность выпадения всех значений, равных или превышающих y – задача аналогична предыдущей, но на этот раз p равно 1/с , умноженным на все возможности, которые удовлетворяют начальному условию. Например, допустим, у нас есть обычный кубик и y = 3 . Мы хотим, чтобы прокатанное значение было либо 6 , 5 , 4 , либо 3 . Тогда переменная p равна 4 · 1/6 = 2/3 , а окончательная вероятность равна P = (2/3)ⁿ .
Вероятность выпадения всех значений, равных или меньших y — этот вариант почти такой же, как и предыдущий, но на этот раз нас интересуют только числа, равные или меньшие нашей цели. Если мы возьмем одинаковые условия ( s=6 , y=3 ) и применим их в этом примере, мы увидим, что значения 1 , 2 и 3 удовлетворяют правилам, а вероятность равно: P = (3 · 1/6)ⁿ = (1/2)ⁿ .
Вероятность выпадения ровно X одинаковые значения (равные y ) из набора — представьте, что у вас есть набор из семи 12-гранных игральных костей, и вы хотите узнать вероятность получения ровно две девятки . Это как-то отличается от предыдущего, потому что только часть всего набора должна соответствовать условиям . Здесь на помощь приходит биномиальная вероятность. Формула биномиальной вероятности:
P(X=r) = nCr · pʳ · (1-p)ⁿ⁻ʳ ,
где r — количество успехов, а nCr — количество комбинаций (также известное как « n выбрать r »).
В нашем примере мы имеем n = 7 , p = 1/12 , r = 2 , nCr = 21 , поэтому окончательный результат: P(X=2) = 21 · (1 /12)² · (11/12)⁵ = 0,09439 или P(X=2) = 9,439% в процентах.

🙋 Более подробную информацию по этой теме вы можете найти в нашем калькуляторе биномиального распределения.

Вероятность выпадения не менее X одинаковых значений (равных y ) из набора — задача очень похожа на предыдущую, но на этот раз результатом является сумма вероятностей для X =2,3,4,5,6,7 . Переходя к числам, мы имеем: P = P(X=2) + P(X=3) + P(X=4) + P(X=5) + P(X=6) + P(X= 7) = 0,11006 = 11,006% . Как и следовало ожидать, результат немного выше. Иногда точная формулировка проблемы увеличивает ваши шансы на успех. 9k&\binom{n}{k}\\ &\binom{r\!-s\!\cdot\!k\!-\!1}{n\!-\!1} \end{split}P(r,n,s)=sn1k=0∑⌊(r−n)/s⌋(−1)k(kn)(n−1r−s⋅k−1 )
Однако мы также можем попробовать решить эту задачу вручную. Один из подходов состоит в том, чтобы найти общее количество возможных сумм. С парой обычных игральных костей мы можем получить 2,3,4,5,6,7,8,9,10,11,12 , но эти результаты не эквивалентны !
Взгляните; есть только один способ получить 2 : 1+1 , но за 4 , есть три разных варианта: 1+3 , 2+2 , 3+1 , а для 12 есть, опять же, только один вариант: 6+6 . Оказывается, 7 является наиболее вероятным результатом с шестью вариантами: 1+6 , 2+5 , 3+4 , 4+3 , 5+2 и 6+ 1 . Количество перестановок с повторениями в этом наборе равно 36 . Наш калькулятор перестановок может быть полезен для поиска перестановок для других типов игральных костей. Мы можем оценить вероятности как отношение благоприятных исходов ко всем возможным исходам: P(2) = 1/36 , P(4) = 3/36 = 1/12 , P(12) = 1/36 , P(7) = 6/36 = 1/6 .
Чем больше игральных костей, тем ближе функция распределения сумм к нормальному распределению. Как и следовало ожидать, по мере увеличения количества игральных костей и граней все больше времени уходит на оценку результата на листе бумаги. К счастью, это не относится к нашему калькулятору вероятности игры в кости!
1. Вероятность выпадения суммы из множества, не ниже X — как и в предыдущей задаче, мы должны найти все результаты, которые соответствуют начальному условию, и разделить их на количество всех возможностей. Учитывая набор из трех десятигранных игральных костей, мы хотим получить сумму не менее 27 . Как мы видим, мы должны сложить все перестановки для 27 , 28 , 29 и 30 , то есть 10, 6, 3 и 1 соответственно. Всего из 1000 возможностей 20 хороших исходов, поэтому конечная вероятность: P(X ≥ 27) = 20/1000 = 0,02 .
2. Вероятность выпадения суммы из множества, не выше X — процедура точно такая же, как и в предыдущей задаче, но складывать нужно только суммы меньше или равные заданной. Имея тот же набор костей, что и выше, какова вероятность того, что выпадет не более 26 ? Если бы вы делали это шаг за шагом, потребовались бы годы, чтобы получить результат (суммировать все 26 сумм). Но, если подумать, мы только что вычислили дополнительное событие в предыдущей задаче. Суммарная вероятность дополнительных событий точно равна 1 , поэтому вероятность здесь равна: P(X ≤ 26) = 1 — 0,02 = 0,98 .
Когда использовать калькулятор вероятности игры в кости?
Существует множество настольных игр, в которых вы по очереди бросаете кубик (или игральные кости), а результаты могут использоваться в различных контекстах. Допустим, вы играете в Dungeons & Dragons и атакуете. Класс брони вашего противника 17 . Вы бросаете 20-гранный кубик, надеясь, что выпадет как минимум 15 с вашим модификатором +2. Этого должно быть достаточно. При этих условиях вероятность успешной атаки равна 0,30 . Если вы знаете шансы на успешную атаку, вы можете выбрать, хотите ли вы атаковать эту цель или выбрать другую с лучшими шансами.
Или, может быть, вы играете в Поселенцы Катана и надеетесь выбросить ровно 8 на двух шестигранных кубиках, так как этот результат принесет вам драгоценные ресурсы. Просто воспользуйтесь нашим калькулятором вероятности в костях, и вы увидите, что вероятность составляет около 0,14 – вам лучше повезти на этом ходу!
Играть или пасовать? — Давай сыграем в игру!
Существуют различные виды игр, например, лотереи, где ваша задача состоит в том, чтобы сделать ставку в зависимости от шансов. Бросание игральных костей является одним из них. Хотя некоторые риски неизбежны, вы можете выбрать наиболее выгодный вариант и максимизировать свои шансы на победу. Взгляните на этот пример.
Представьте, что вы играете в игру, в которой у вас есть один из трех вариантов на выбор , а именно:
- Сумма пяти десятигранных костей не менее 30 ;
- Сумма пяти 12-гранных костей не превышает 28 ;
- Сумма пяти 20-гранных костей не меньше 59 .
Вы выиграете, только если выпадет выбранный вами вариант. Вы также можете отказаться, если чувствуете, что ничего из этого не произойдет. Интуитивно трудно оценить наиболее вероятный успех, но с нашим калькулятором вероятности в костях для оценки всех вероятностей требуется всего лишь мгновение ока.
Полученные значения:
- P₁ = 0,38125 для 10-гранного игрального кубика;
- P₂ = 0,3072 для 12-гранной кости; и
- P₃ = 0,3256 для 20-гранной кости.
Вероятность успешного прохода равна произведению дополнительных событий остальных вариантов:
- P₄ = (1-P₁) · (1-P₂) · (1-P₃) = 0,61875 · 0,6928 · 0,6744 = 0,2891 .
Мы видим, что самый благоприятный вариант — первый, а прохождение — наименее вероятное событие. Мы не можем гарантировать, что вы всегда будете выигрывать, но мы настоятельно рекомендуем вам выбрать для игры 10-гранный набор костей.
Часто задаваемые вопросы
Что такое вероятность?
Вероятность определяет, насколько вероятны определенные события . Простая формула для вероятности: число желаемых исходов/количество возможных исходов . В настольных играх или азартных играх вероятность выпадения костей используется для определения вероятности выпадения определенного числа , например, какова вероятность получения определенного числа одним кубиком?
Сколько возможных исходов может быть при бросании двух игральных костей?
Есть 36 исходов при бросании двух игральных костей . Для одного игрального кубика имеется шесть граней, и для любого броска есть шесть возможных исходов . Для две кости , вы должны перемножить количество возможных исходов вместе, чтобы получить 6 × 6 = 36 . При последующих бросаниях просто умножьте результат на 6 . Если вы используете кости другой формы, вместо 6 введите число их граней .
Какова вероятность того, что при броске 2 игральных костей выпадет 7?
Это 1/6 или 0,1666667 . Предположим, что всего 7 встречается хотя бы один раз . Для 2 игральных костей есть 6 способов бросить сумму 7 — (1,6), (2,5), (3,4), (4,3), (5,2), (6 ,1) . Общее количество комбинаций для пары кубиков равно 36 . Таким образом, вероятность суммирования до 7 равна 6/36 = 1/6 = 0,1666667 .
Сколько раз я выбрасываю 5 на паре игральных костей?
20 . Предположим, что пару игральных костей бросают 180 раз . У вас есть 4 способа получить сумму 5 — (1,4), (2,3), (3,2) и (4,1) . Вероятность выпадения суммы 5 равна 4/36 = 1/9 . Ожидаемое число за 180 бросков равно 180 × (1/9) = 20 . Вы будете кидать сумму 5 не менее 20 раз .
Могу ли я всегда выбрасывать 6 на кубике?
Нет , это всегда вопрос удачи, но вы можете увеличить свои шансы используя некоторые хитрости:
1. Поместите указательный и большой пальцы на цифры, расположенные на противоположных сторонах , открывая 1 и 6 .
2. Медленно бросайте кости и надейтесь, что кости выпадут правильно.
Хитрость в том, что вы позволяете бросать кости с оставшимися числами, создавая более высокую вероятность выпадения числа 6 .
Wojciech Sas, PhD
Выберите тип и количество игральных костей
Тип игральных костей
Общее количество костей
Выберите условия — Правила игры
Я хочу получить:
Значение костей, которое я хочу получить:
. ..что приводит к…
Вероятность получения любого значения из the dice
Ознакомьтесь с 22 похожими калькуляторами теории вероятностей и шансов 🎲
Точность Теорема Байеса Парадокс дня рождения… Еще 19
Калькулятор куба x³
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Использование
Найдите значение числа n в кубе. Введите положительные или отрицательные целые числа или десятичные числа или научную нотацию E.
Кубирование отрицательных чисел
При кубировании отрицательных чисел ответ всегда будет отрицательным. В этом калькуляторе вам не нужно использовать круглые скобки при вводе, потому что вы все равно получите правильный ответ, хотя вы должны знать, что ниже показано, как ваши вводы на самом деле интерпретируются калькулятором.
- -2³ означает -(2 × 2 × 2) = -8
- -(2)³ означает -(2 × 2 × 2) = -8
- (-2)³ означает (-2 × -2 × -2) = -8
Когда выражение степени записывается с положительным значением, таким как 4³, большинству легко понять, что это означает 4 × 4 × 4 = 64
отрицательное значение без круглых скобок означает неоднозначность. Для разных людей это имеет разное значение.
Различные возможные интерпретации -4³:
1. минус (4 в кубе) или -(4)³ = -(4 × 4 × 4) = -64
2. (минус 4) в кубе или (-4 )³ = (-4 × -4 × -4) = -64
Используйте круглые скобки, чтобы четко указать, какое вычисление вы действительно хотите выполнить. Скобки не изменяют ваши результаты, когда показатель степени нечетен, например, 3, но они имеют явное значение, когда показатель степени четен, например, 2. Калькулятор площади для -4²
Куб
Число n в кубе записывается как n³ и n³ = n × n × n.