Расчет онлайн г образной лестницы: Онлайн расчёт П-образной лестницы с забежными ступенями
Расчет изготовления лестниц — Онлайн-Калькулятор
- Каталог
- Деревянные
- Винтовые
- Модульные
- Металлические
- Чердачные
- Крыльцо
- Наши работы
- Заказать замер
- Онлайн-калькулятор лестницы
Контактная информация
Москваул. Уткина, д.48, стр.4
8 (495) 374-57-17 Круглосуточно
zakaz@lestnicy-prosto.
Расчет лестниц с нашими специалистами – просто!
Планируя отделку и обустройство своего дома, желательно на самом раннем этапе предусмотреть наличие лестницы. Оптимальным решением является случай, при котором лестница является неотъемлемой частью всего проекта. При таком варианте расчет лестницы производиться заранее, она вписывается гармонично в обустраиваемое пространство и отвечает всем потребностям заказчика.Как показывает практика, в большинстве случаев владельцы дома полагаются на рекомендации строителей только отчасти и отводят под лестницу немного места в надежде, что она компактно впишется и будет при этом удобной. Строители или проектировщики, тоже, к сожалению, не всегда уделяют должное внимание такому важному элементу дома, как лестница. Отсюда возникают определенные трудности и ограничения при расчете лестницы.
Наши специалисты будут рады помочь с расчетом лестницы на любом этапе строительства и проектирования дома!
С чего начать?
Мы предлагаем, прежде всего, определиться с размерами необходимыми для расчета лестницы.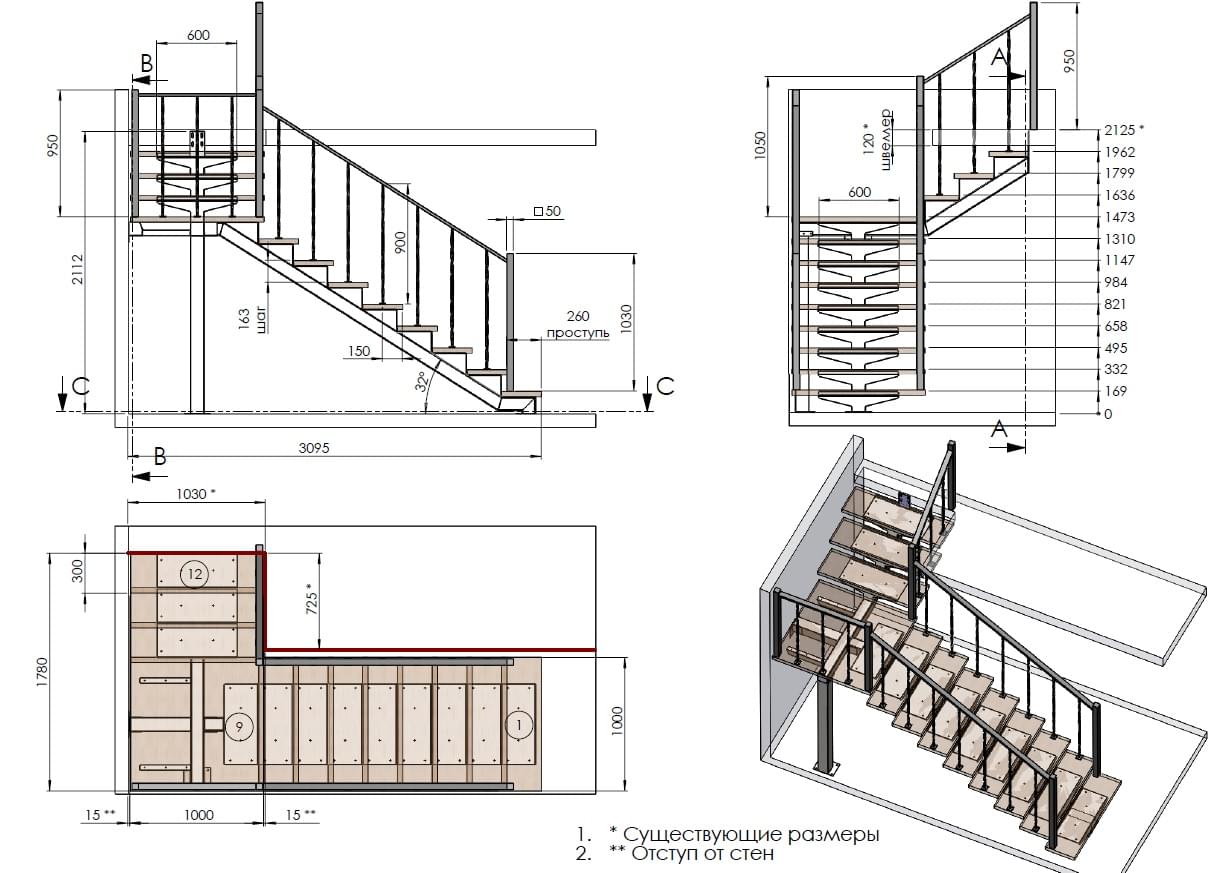 Для этого можно воспользоваться услугами наших замерщиков или самостоятельно снять замеры следующих параметров:
Для этого можно воспользоваться услугами наших замерщиков или самостоятельно снять замеры следующих параметров: – высота лестницы от пола нижнего этажа до пола верхнего этажа – толщина перекрытия
– длина и ширина проема
– габариты в плане (длина и ширина площади отводимой под лестницу)
– возможные помехи (двери, окна, батареи и т.д.)
Далее
Нужно определить форму будущей лестницы:Винтовые лестницы
Г-образные лестницы
П-образные лестницы
Забежные лестницы
Маршевые лестницы
Затем
Сделать выбор по материалу: деревянные, на металлокаркасе, металлические. Если лестница деревянная, то нужно определиться с породой:Лестницы из сосны
Лестницы из лиственницы
Лестницы из березы
Лестницы из бука
Лестницы из ясеня
Лестницы из дуба
В итоге!
На основании всех этих данных наш менеджер бесплатно сделает проект, который будет учитывать возможности помещения, исходя из представленных параметров, и все пожелания по комфорту и эстетики вашей будущей лестницы!Как рассчитать лестницу в онлайн калькуляторе — Производство лестниц в Минске LascalaGrande
Как сделать расчет любого вида лестниц в специальном онлайн конструкторе.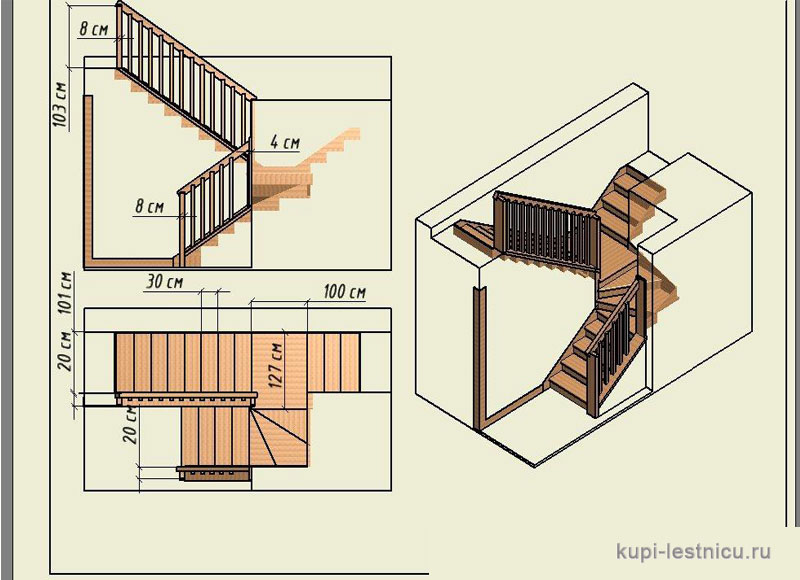 Обзор функционала калькулятора лестниц и принципы его работы.
Обзор функционала калькулятора лестниц и принципы его работы.
Чтобы самостоятельно сделать расчёт деревянной или металлической лестниц мы разработали online конструктор, который позволяет сделать расчёт или чертежи лестниц без особых усилий. Он поможет быстро рассчитать все необходимые параметры конструкции для более точной оценки стоимости лестницы или для самостоятельного изготовления лестниц. Разберемся, как он работает.
Совершив переход на страницу с конструктором-калькулятором, мы видим следующее (рис. 1):
рис.1
Первый шаг (отмечен 1 на рис. 1) – определить тип будущей лестницы.
Разберем пример. Рассчитаем простую конструкцию Г-образной формы (Дачная лестница). Используем упрощенный алгоритм, понятный любому пользователю, даже без технического образования:
- В соответствующих полях (рис.1, отметка 2) вводим данные: высоту помещения и ширину, длину проёма, выделенного для размещения конструкции лестницы.
- Нажимаем «Рассчитать» (рис.
 1, отметка 3). Справа выводится полученный результат – схематическое изображение лестницы с видом сверху, идеально вписывающийся в заданные размеры. После проверки размеров переходим к следующему шагу.
1, отметка 3). Справа выводится полученный результат – схематическое изображение лестницы с видом сверху, идеально вписывающийся в заданные размеры. После проверки размеров переходим к следующему шагу. - Нажимаем «Чертеж» (рис. 1, отметка 4). Программа открывает дополнительное окно с полноценным чертежом выбранной лестницы (рис. 2). Здесь отражаются все размеры: высота ступеней, ширина изделия, и прочими.
рис.2. Чертеж вашей лестницы.
Чертежи полученной лестницы можно распечатать. Для печати чертежа нажмите CTRL+P. Чертеж можно использовать для заказа изготовления лестницы.
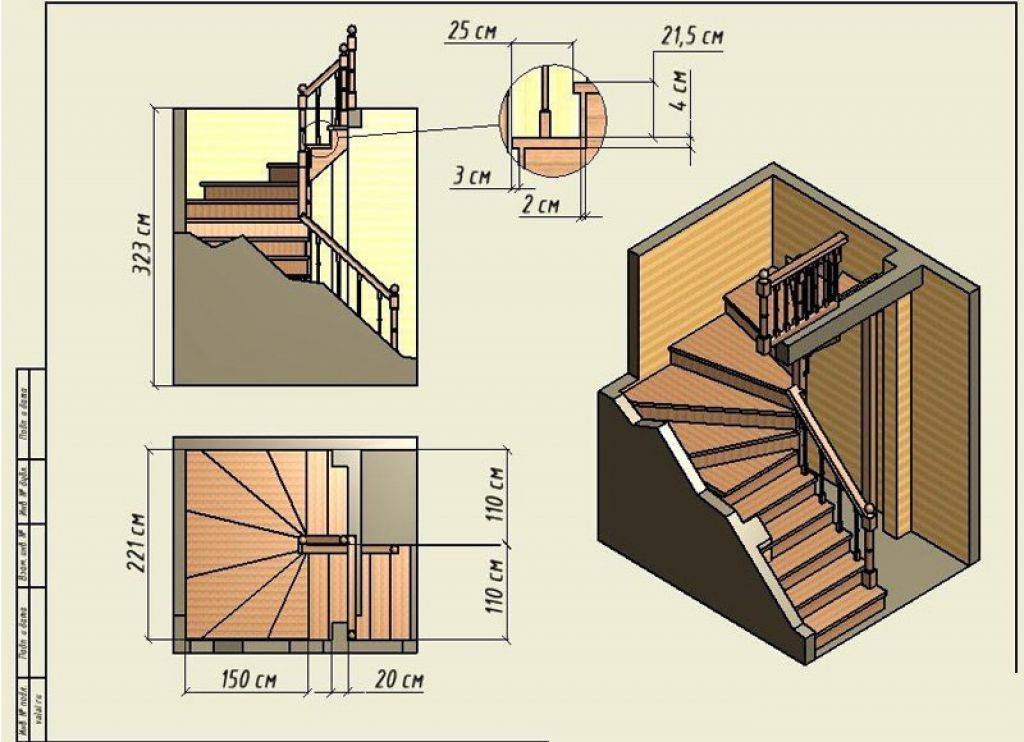
Онлайн расчёт П-образной лестницы (рис.3).
Выбираем вкладку«П-образная лестница» на начальной странице конструктора. В соответствующих полях (рис.3 отметка 1) вписываем габариты желаемого изделия, а не комнаты.
рис.3. Расчет П-образной лестницы
Вводится высота, ширина конструкции (а не помещения), выбирается желаемое число ступеней (приложение автоматически рассчитает подъем каждой ступени). После этого следует нажать «Рассчитать» и проверить появившийся справа результат (схематическое изображение с видом сверху).
После этого следует нажать «Рассчитать» и проверить появившийся справа результат (схематическое изображение с видом сверху).
При желании можно добавить ограждения с одной или обеих сторон, на отдельных участках.
Во вкладке «Дизайн» (рис. 3, отметка 2) доступен выбор расцветки, внешнего вида балясин, поручней, прочих элементов. При нажатии на «?» можно посмотреть изображения с подсказками.
Значительное влияние на стоимость изделия оказывает выбранный материал. У вас есть возможность использовать разную древесину для каждого элемента изделия (например, все из сосны, березы, а ступени из дуба). Это позволит сократить издержки.
После выбора внешнего вида, цвета, материалов нажимаем сначала «Рассчитать», а потом «Чертеж». Печатаем полученный чертеж конструктора лестниц с подробным описанием, схематическим и 3D-изображением желаемой лестницы.
Он-лайн калькулятор лестниц позволяет рассчитать и более сложные виды лестниц, – например, винтовую лестницу (рис.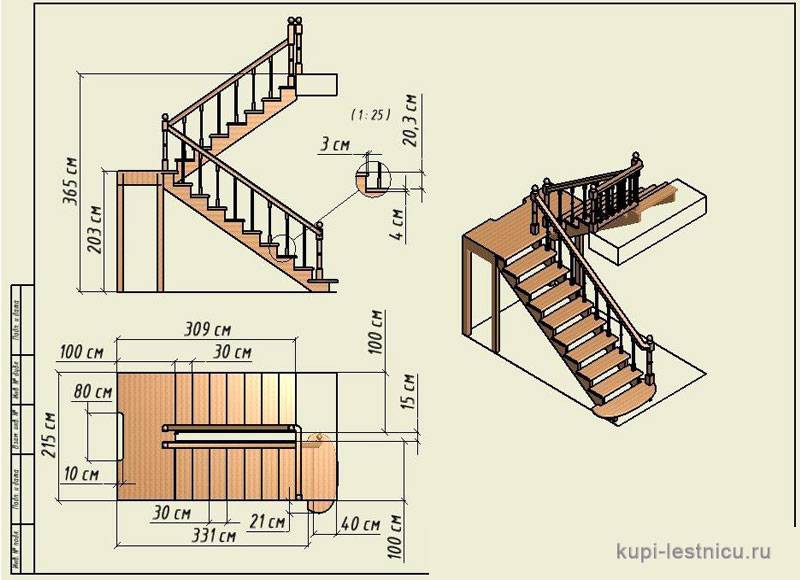
рис.5. Чертежи винтовой лестницы.
Вы можете «покрутить» различные параметры. Например, убедиться, что чем больше «закрутишь» винтовую лестницу (например, до 270°, а лучше, до 360°), то получишь более удобную винтовую лестницу – с широкими, удобными ступенями. Остальной расчет винтовой лестницы аналогичен таковому для всех остальных лестниц.
Повышенного внимания заслуживают расчеты прямой лестницы (рис. 6).
рис.6
Здесь используется наиболее простой алгоритм расчетов идентичный дачной Г-образной лестнице. Нужно вводить параметры помещения, в котором она будет использоваться, а не самого изделия. Программа самостоятельно выполнит все необходимые расчеты и идеально впишет вашу лестницу в нужные размеры проёма. Более того, – если проем слишком мал (см.рис.7,- длина проема всего лишь 2 метра 30 см),- программа сама предложит вам установить «лестницу с Гусиным шагом», как самую малогабаритную.
После ввода параметров не забывайте нажимать «Рассчитать», чтобы программа произвела расчеты и кнопку «Чертеж» для получения подробной версии, которую можно отправить на принтер для печати через сочетание клавиш CTRL+P.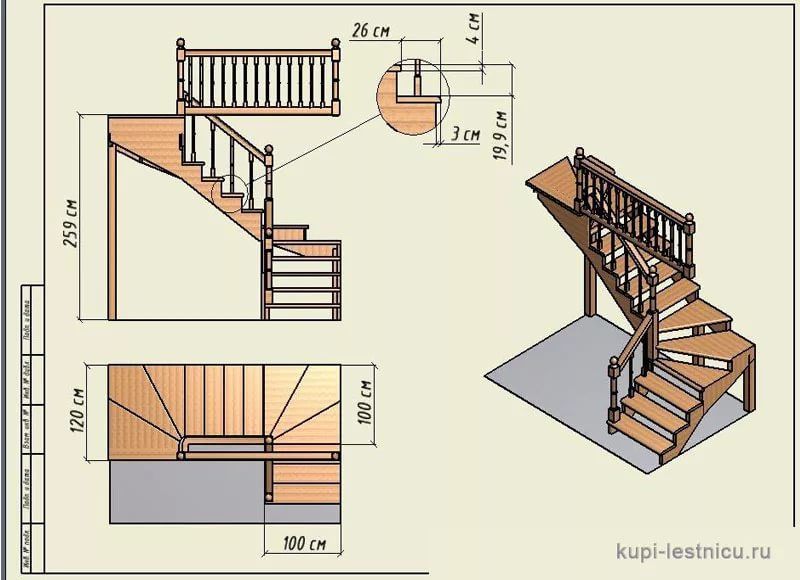 Если вы хотите заказать лестницу у нас – используйте полученные чертежи.
Если вы хотите заказать лестницу у нас – используйте полученные чертежи.
рис.7. Лестница с гусиным шагом.
Особенность нашего конструктора лестниц в отличии от других, онлайн программ расчета лестниц, в том, что наш калькулятор сделан для расчета именно деревянных лестниц, учитывает все детали конструктива (место под тетиву лестницы, её ограждение; конструктив забежных ступеней из дерева, и т.п.), – в отличии от других конструкторов, которые считает просто лестницу, – одинаково как для лестниц из бетона, либо металлических лестниц.
Таким образом, наш калькулятор лестниц LaScalaGrande позволяет быстро, всего за пару минут, рассчитать деревянную лестницу онлайн, даже если вы не опытный столяр, а обычный дачник, рассчитывающий лестницу для изготовления своими руками, себе в дом…
[/fusion_text]Расчет прямой лестницы на ломаном скате онлайн
См. также
Выбрать чертеж:
- Чертеж лестницы (вид сбоку)
- Косоур (шаблон)
- Чертеж лестницы (вид сверху)
- Чертеж лестницы (вид спереди) )
- Прямой шаг
- Подступенки прямых шагов
Расстояние: 0
Результаты расчета Размеры лестницыУгол: 32,44 °
Формула удобной лестницы (R + G): 45,41 см
9000 8Формула Блонделя (2R + G): 63,06 см
Подъем: 17,65 см
Глубина протектора: 33,56 см
Ход: 27,76 см 9 0003
Количество ступеней: 16 шт.

Ширина лестницы: 100 см
Высота трубы: 6 см
Ширина трубки: 4 см
Общая длина стальной трубки: 1813,11 см
Всего деталей: 64 шт.
Глубина ступени: 33,56 см
Длина: 100 см
Толщина: 4 см
Количество: 16 шт.
Объем дерева: 0,215 м3
Ручной Ширина поручня: 8 см
Толщина поручня: 4 см
Длина поручня: 542,32 см
Объем дерева: 0,017 м3
Левый поворот: выбрано
Общая высота: 300 см
Общая длина: 450 см
Ширина лестницы: 100 см
Количество: 16 шт.

Толщина: 4 см
Выступ (нахлест протектора): 4 см
Верхняя ступень ниже уровня 2-го этажа: 1 см
Трубка Высота: 6 см
Ширина трубки: 4 см
Высота: 4 см
Ширина: 4 см
Толщина: 1,8 см
Высота поручня: 90 см
Ширина балясины: 5 см
Толщина поручня: 4 см
Ширина поручня: 8 см
Толщина: 20 см
Обратите внимание
- Значения выделены зеленым цвет являются допустимыми значениями.

- Значения, выделенные оранжевым цветом , имеют незначительные отклонения от нормы.
- Значения, выделенные красным цветом , представляют собой значения, которые подвергают конструкцию риску разрушения или делают ее использование неудобным.
Линейная регрессия в R | Пошаговое руководство и примеры
Опубликован в 25 февраля 2020 г. к Ребекка Беванс. Отредактировано 15 ноября 2022 г.
Линейная регрессия — это модель регрессии, в которой для описания отношений между переменными используется прямая линия. Он находит линию наилучшего соответствия вашим данным путем поиска значения коэффициента (коэффициентов) регрессии, которое минимизирует общую ошибку модели.
Существует два основных типа линейной регрессии:
- Простая линейная регрессия использует только одну независимую переменную
- Множественная линейная регрессия использует две или более независимых переменных
В этом пошаговом руководстве мы проведем вас через линейную регрессию в R, используя два примера наборов данных.
Набор данных простой регрессии Набор данных множественной регрессии
Содержание
- Начало работы с R
- Шаг 1: Загрузите данные в R
- Шаг 2: Убедитесь, что ваши данные соответствуют предположениям
- Шаг 3: Выполните анализ линейной регрессии
- Шаг 4: Проверьте гомоскедастичность
- Шаг 5: Визуализируйте результаты с помощью графика
- Шаг 6: Сообщите о своих результатах
Начало работы в R
Начните с загрузки R и RStudio. Затем откройте RStudio и нажмите File > New File > R Script .
Затем откройте RStudio и нажмите File > New File > R Script .
По мере прохождения каждого шага вы можете копировать и вставлять код из текстовых полей прямо в свой скрипт. Чтобы запустить код, выделите строки, которые вы хотите запустить , и нажмите кнопку Выполнить в правом верхнем углу текстового редактора (или нажмите ctrl + введите на клавиатуре).
Чтобы установить необходимые для анализа пакеты, запустите этот код (это нужно сделать только один раз):
install.packages("ggplot2")
install.packages("dplyr")
install.packages("broom")
install.packages("ggpubr") Затем загрузите пакеты в среду R, запустив этот код (нужно делать это каждый раз при перезапуске R):
библиотека (ggplot2)
библиотека (dplyr)
библиотека (broom)
библиотека (ggpubr) Шаг 1: Загрузите данные в R
Выполните следующие четыре шага для каждого набора данных:
- В RStudio перейдите к пункту Файл > Импорт набора данных > Из текста (база) .

- Выберите файл данных, который вы загрузили (income.data или heart.data), и откроется окно Import Dataset .
- В окне Data Frame вы должны увидеть столбец X (индекс) и столбцы со списком данных для каждой из переменных (доход и счастье или езда на велосипеде, курение и болезнь сердца).
- Нажмите кнопку Import , и файл должен появиться в вашем Вкладка Environment в верхней правой части экрана RStudio.
После того, как вы загрузили данные, проверьте правильность их считывания с помощью summary() .
Простая регрессия
summary(income.data) Поскольку обе наши переменные являются количественными, при запуске этой функции мы видим в консоли таблицу с числовой сводкой данных. Это говорит нам о минимальном, медианном, среднем и максимальном значениях независимой переменной (доход) и зависимой переменной (счастье):
Множественная регрессия
summary(heart. data)
data) Опять же, поскольку переменные являются количественными, запуск кода дает числовую сводку данных для независимых переменных (курение и езда на велосипеде) и зависимой переменной (болезнь сердца):
Получайте отзывы о языке, структуре и форматировании
Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание:
- Академический стиль
- Расплывчатые предложения
- Грамматика
- Согласованность стиля
См. пример
Шаг 2. Убедитесь, что ваши данные соответствуют предположениям
Мы можем использовать R, чтобы проверить, соответствуют ли наши данные четырем основным предположениям для линейной регрессии.
Простая регрессия
- Независимость наблюдений (отсутствие автокорреляции)
Поскольку у нас есть только одна независимая переменная и одна зависимая переменная, нам не нужно проверять какие-либо скрытые взаимосвязи между переменными.
Если вы знаете, что у вас есть автокорреляция внутри переменных (т. е. несколько наблюдений за одним и тем же испытуемым), не используйте простую линейную регрессию! Вместо этого используйте структурированную модель, например линейную модель со смешанными эффектами.
- Нормальность
Чтобы проверить, подчиняется ли зависимая переменная нормальному распределению, используйте функцию hist() .
история(доход.данные$счастье) Наблюдения имеют примерно колоколообразную форму (больше наблюдений в середине распределения, меньше на хвостах), поэтому мы можем продолжить линейную регрессию.
- Линейность
Связь между независимой и зависимой переменной должна быть линейной. Мы можем проверить это визуально с помощью графика рассеяния, чтобы увидеть, можно ли описать распределение точек данных прямой линией.
сюжет(счастье ~ доход, данные = доход. данные)
данные) Зависимость выглядит примерно линейной, поэтому мы можем продолжить линейную модель.
- Гомоскедастичность (однородность дисперсии)
Это означает, что ошибка прогноза существенно не меняется в диапазоне прогноза модели. Мы можем проверить это предположение позже, после подгонки линейной модели.
Множественная регрессия
- Независимость наблюдений (отсутствие автокорреляции)
Используйте функцию cor() , чтобы проверить взаимосвязь между вашими независимыми переменными и убедиться, что они не слишком сильно коррелированы.
cor(heart.data$езда на велосипеде, heart.data$курение) Когда мы запускаем этот код, результат равен 0,015. Корреляция между ездой на велосипеде и курением невелика (0,015 — корреляция всего 1,5%), поэтому мы можем включить в нашу модель оба параметра.
- Нормальность
Используйте функцию hist() , чтобы проверить, соответствует ли ваша зависимая переменная нормальному распределению.
гист(сердце.данные$сердечная.болезнь) Распределение наблюдений примерно колоколообразное, поэтому мы можем продолжить линейную регрессию.
- Линейность
Мы можем проверить это, используя две диаграммы рассеяния: одну для езды на велосипеде и сердечных заболеваний, а другую для курения и сердечных заболеваний.
plot(heart.disease ~ езда на велосипеде, data=heart.data) plot(heart.disease ~ курение, data=heart.data) Хотя взаимосвязь между курением и сердечными заболеваниями немного менее ясна, она по-прежнему кажется линейной. Мы можем продолжить линейную регрессию.
- Гомоскедастичность
Мы проверим это после изготовления модели.
Шаг 3. Выполните анализ линейной регрессии
Теперь, когда вы определили, что ваши данные соответствуют предположениям, вы можете выполнить линейный регрессионный анализ, чтобы оценить связь между независимыми и зависимыми переменными.
Простая регрессия: доход и счастье
Давайте посмотрим, существует ли линейная зависимость между доходом и счастьем в нашем опросе 500 человек с доходами от 15 до 75 тысяч долларов, где счастье измеряется по шкале от 1 до 10.
Для выполнения простого линейного регрессионного анализа и проверки результатов необходимо запустить две строки кода. Первая строка кода создает линейную модель, а вторая строка выводит сводку модели:
.доход.счастье.лм <- лм(счастье ~ доход, данные = доход.данные) резюме (доход.счастье.lm)
Вывод выглядит следующим образом:
В этой выходной таблице сначала представлено уравнение модели, а затем обобщены остатки модели (см. шаг 4).
В разделе Коэффициенты показано:
- Оценки ( Estimate ) для параметров модели – значение точки пересечения y (в данном случае 0,204) и расчетное влияние дохода на счастье (0,713).
- Стандартная ошибка расчетных значений ( Std.
 Error ).
Error ). - Тестовая статистика ( t значение , в данном случае t статистика).
- Значение p ( Pr(>| t | ) ), также известная как вероятность нахождения данной статистики t , если нулевая гипотеза об отсутствии связи верна.
Последние три строки — это диагностика модели — самое важное, что нужно отметить, — это p значение (здесь это 2.2e-16, или почти ноль), которое укажет, хорошо ли модель соответствует данным.
Исходя из этих результатов, мы можем сказать, что существует значительная положительная связь между доходом и счастьем ( p значение <0,001), с увеличением счастья на 0,713 единицы (+/- 0,01) на каждую единицу увеличения дохода.
Множественная регрессия: езда на велосипеде, курение и болезни сердца
Давайте посмотрим, существует ли линейная связь между поездками на работу на велосипеде, курением и сердечными заболеваниями в нашем воображаемом опросе 500 городов. Показатели поездок на работу на велосипеде колеблются от 1 до 75%, курят от 0,5 до 30% и сердечно-сосудистых заболеваний от 0,5% до 20,5%.
Показатели поездок на работу на велосипеде колеблются от 1 до 75%, курят от 0,5 до 30% и сердечно-сосудистых заболеваний от 0,5% до 20,5%.
Чтобы проверить взаимосвязь, мы сначала подогнали линейную модель с болезнью сердца в качестве зависимой переменной и ездой на велосипеде и курением в качестве независимых переменных. Запустите эти две строки кода:
heart.disease.lm<-lm(heart.disease ~ езда на велосипеде + курение, данные = heart.data) резюме (heart.disease.lm)
Вывод выглядит следующим образом:
Предполагаемое влияние езды на велосипеде на болезни сердца составляет -0,2, а предполагаемое влияние курения - 0,178.
Это означает, что на каждый 1% увеличения количества поездок на работу на велосипеде приходится коррелированное снижение на 0,2% случаев сердечно-сосудистых заболеваний. Между тем, на каждый 1% увеличения курения приходится 0,178% увеличения частоты сердечных заболеваний.
Стандартные ошибки для этих коэффициентов регрессии очень малы, а статистика t очень велика (-147 и 50,4 соответственно). Значения p отражают эти небольшие ошибки и большую статистику t . Для обоих параметров почти нулевая вероятность того, что этот эффект обусловлен случайностью.
Значения p отражают эти небольшие ошибки и большую статистику t . Для обоих параметров почти нулевая вероятность того, что этот эффект обусловлен случайностью.
Помните, что эти данные составлены для этого примера, поэтому в реальной жизни эти отношения не были бы такими четкими!
Шаг 4. Проверка гомоскедастичности
Прежде чем приступить к визуализации данных, мы должны убедиться, что наши модели соответствуют предположению о гомоскедастичности линейной модели.
Простая регрессия
Мы можем запустить plot(income.happiness.lm) , чтобы проверить, соответствуют ли наблюдаемые данные предположениям нашей модели:
par(mfrow=c(2,2))
plot(income.happiness.lm)
par(mfrow=c(1,1)) Обратите внимание, что команда par(mfrow()) разделит Помещает окно в число строк и столбцов, указанное в скобках. Так par(mfrow=c(2,2)) делит его на две строки и два столбца. Чтобы вернуться к построению одного графика во всем окне, снова задайте параметры и замените (2,2) на (1,1).
Чтобы вернуться к построению одного графика во всем окне, снова задайте параметры и замените (2,2) на (1,1).
Это остаточные участки, созданные кодом:
Остатки — необъяснимая дисперсия. Это не совсем то же самое, что ошибка модели, но они рассчитываются на ее основе, поэтому смещение в остатках также указывает на смещение в ошибке.
Самое важное, на что следует обратить внимание, это то, что все красные линии, представляющие среднее значение остатков, в основном горизонтальны и сосредоточены вокруг нуля. Это означает, что в данных нет выбросов или погрешностей, которые сделали бы линейную регрессию недействительной.
На графике Normal Q-Qplot в правом верхнем углу мы видим, что реальные невязки из нашей модели почти полностью совпадают с теоретическими остатками идеальной модели.
Основываясь на этих остатках, мы можем сказать, что наша модель удовлетворяет предположению о гомоскедастичности.
Множественная регрессия
Опять же, мы должны проверить, что наша модель действительно хорошо подходит для данных, и что у нас нет большой вариации ошибки модели, выполнив этот код:
par(mfrow=c(2,2))
plot(heart. disease.lm)
disease.lm)
par(mfrow=c(1,1)) Вывод выглядит следующим образом:
Как и в случае с нашей простой регрессией, остатки не показывают смещения, поэтому мы можем сказать, что наша модель соответствует предположению о гомоскедастичности.
Шаг 5. Визуализируйте результаты с помощью графика
Затем мы можем построить данные и линию регрессии из нашей модели линейной регрессии, чтобы можно было поделиться результатами.
Простая регрессия
Выполните 4 шага, чтобы визуализировать результаты простой линейной регрессии.
- Нанесение точек данных на график
доход.граф<-ggplot(доход.данные, aes(x=доход, y=счастье))+
геометрическая_точка()
доход.граф
- Добавить линию линейной регрессии к графическим данным
Добавьте линию регрессии с помощью geom_smooth() и введите lm в качестве метода создания линии. Это добавит линию линейной регрессии, а также стандартную ошибку оценки (в данном случае +/- 0,01) в виде светло-серой полосы, окружающей линию:
Это добавит линию линейной регрессии, а также стандартную ошибку оценки (в данном случае +/- 0,01) в виде светло-серой полосы, окружающей линию:
доход.граф <- доход.граф + geom_smooth (метод = "lm", col = "черный") доход.граф
- Добавьте уравнение для линии регрессии.
доход.граф <- доход.граф + stat_regline_equation (label.x = 3, label.y = 7) доход.график
- Подготовить график к публикации
Мы можем добавить некоторые параметры стиля с помощью theme_bw() и создать собственные метки с помощью labs() .
доход.граф +
тема_bw() +
labs(title = "Сообщаемое счастье как функция дохода",
х = «Доход (х 10 000 долларов США)»,
y = "Оценка счастья (от 0 до 10)")
Получается готовый график, который вы можете включить в свои документы:
Множественная регрессия
Этап визуализации для множественной регрессии сложнее, чем для простой регрессии, потому что теперь у нас есть два предиктора. Одним из вариантов является построение плоскости, но их трудно читать и они не часто публикуются.
Одним из вариантов является построение плоскости, но их трудно читать и они не часто публикуются.
Мы попробуем другой метод: построить график взаимосвязи между ездой на велосипеде и сердечными заболеваниями при разном уровне курения. В этом примере курение будет рассматриваться как фактор с тремя уровнями только для целей отображения отношений в наших данных.
Необходимо выполнить 7 шагов.
- Создайте новый фрейм данных с информацией, необходимой для построения модели
Используйте функцию expand.grid() для создания кадра данных с указанными вами параметрами. В рамках этой функции мы будем:
- Создайте последовательность от самого низкого до самого высокого значения ваших наблюдаемых данных о езде на велосипеде;
- Выберите минимальное, среднее и максимальное значения курения, чтобы получить 3 уровня курения, по которым можно прогнозировать частоту сердечных заболеваний.
plotting.data<-expand.grid( езда на велосипеде = последовательность (мин (сердце. данные $ езда на велосипеде), макс (сердце. данные $ езда на велосипеде), длина. выход = 30), курение = c (мин (сердце. данные $ курение), среднее (сердце. данные $ курение), макс (сердце. данные $ курение)))
Это не создаст ничего нового в вашей консоли, но вы должны увидеть новый фрейм данных на вкладке Environment . Нажмите на нее, чтобы просмотреть.
- Предсказание значений болезни сердца на основе вашей линейной модели
Далее мы сохраним наши «предсказанные значения y» в качестве нового столбца в только что созданном наборе данных.
plotting.data$predicted.y <- прогнозировать.lm(heart.disease.lm, newdata=ploting.data)
- Количество копченостей округлить до двух знаков после запятой
Это облегчит чтение легенды в дальнейшем.
plotting.data$smoking <- round(plotting.data$smoking, digits = 2)
- Измените переменную «курение» на коэффициент
Это позволяет нам построить график взаимодействия между ездой на велосипеде и сердечными заболеваниями на каждом из трех выбранных нами уровней курения.
plotting.data$smoking <- as.factor(plotting.data$smoking)
- Постройте исходные данные
heart.plot <- ggplot(heart.data, aes(x=езда на велосипеде, y=heart.disease)) + геометрическая_точка() сердце.сюжет
- Добавьте линии регрессии
сердце.участок <- сердце.участок + geom_line(data=ploting.data, aes(x=велосипед, y=прогноз.y, цвет=курение), размер=1,25) сердце.сюжет
- Подготовить график к публикации
сердце.участок <-
сердце.сюжет +
тема_bw() +
labs(title = "Уровень сердечно-сосудистых заболеваний (% населения)\n в зависимости от поездок на работу на велосипеде и курения",
x = "Езда на работу на велосипеде (% населения)",
y = «Болезнь сердца (% населения)»,
color = "Курение\n (% населения)")
сердце. сюжет
сюжет
Поскольку этот график имеет два коэффициента регрессии, функция stat_regline_equation() здесь не работает. Но если мы хотим добавить нашу модель регрессии на график, мы можем сделать это следующим образом:
heart.plot + annotate(geom="text", x=30, y=1,75, label="= 15 + (-0,2*езда на велосипеде) + (0,178*курение)")
Это готовый график, который вы можете включить в свои документы!
Шаг 6. Сообщите о результатах
В дополнение к графику включите краткое пояснение результатов регрессионной модели.
Сообщив результаты простой линейной регрессии, мы обнаружили значимую связь между доходом и счастьем ( p < 0,001, R 2 = 0,73 ± 0,0193) с увеличением сообщаемого счастья на 0,73 единицы на каждые 10 000 долларов увеличения дохода. Представление результатов множественной линейной регрессии. В нашем обзоре 500 городов мы обнаружили значимые взаимосвязи между частотой поездок на работу на велосипеде и частотой сердечных заболеваний, а также частотой курения и частотой сердечных заболеваний (9).


 1, отметка 3). Справа выводится полученный результат – схематическое изображение лестницы с видом сверху, идеально вписывающийся в заданные размеры. После проверки размеров переходим к следующему шагу.
1, отметка 3). Справа выводится полученный результат – схематическое изображение лестницы с видом сверху, идеально вписывающийся в заданные размеры. После проверки размеров переходим к следующему шагу.
 data)
data)  данные)
данные)  Error ).
Error ). disease.lm)
disease.lm)  data<-expand.grid(
езда на велосипеде = последовательность (мин (сердце. данные $ езда на велосипеде), макс (сердце. данные $ езда на велосипеде), длина. выход = 30),
курение = c (мин (сердце. данные $ курение), среднее (сердце. данные $ курение), макс (сердце. данные $ курение)))
data<-expand.grid(
езда на велосипеде = последовательность (мин (сердце. данные $ езда на велосипеде), макс (сердце. данные $ езда на велосипеде), длина. выход = 30),
курение = c (мин (сердце. данные $ курение), среднее (сердце. данные $ курение), макс (сердце. данные $ курение)))  data$smoking <- round(plotting.data$smoking, digits = 2)
data$smoking <- round(plotting.data$smoking, digits = 2)
 сюжет
сюжет