Сколько теса в кубе штук: Сколько досок в кубе? (таблица) Сколько в кубе досок 6 метров — формула, калькулятор онлайн

Содержание

Сколько необрезной доски в кубе таблица

Главная » Статьи » Сколько необрезной доски в кубе таблица

Сколько штук необрезных досок в 1 кубе — таблица – «ЯсенПень»™

Кубатурник круглого леса

Сколько бруса в кубе

Сколько досок в кубе

Сколько необрезных досок в кубе

Свойства древесины

Плотность, вес, масса древесины

Размеры досок и бруса

Калькулятор бруса и доски на дом

Калькулятор обрезного бруса

Калькулятор профилированного бруса

Калькулятор обрезной доски

Обрезной брус

Профилированный брус

Обрезная доска

Необрезная доска имеет большой разбег по ширине на противоположных концах, поэтому при расчете необрезной доски в формулу нужно подставлять среднюю ширину. Среднюю ширину необрезных досок измеряют на середине длины как полусумму ширин обеих пластей (концов доски) без учета коры и луба. Результат измерения округляют до 10 мм, доли до 5 мм не учитывают, а доли 5 мм и более считают за 10 мм.

Размер необрезной доски Объем 1-й доски Досок в 1-ом кубе в штуках

Доска 25х6000	0,0294 м³	34 шт.
Доска 40х6000	0,05 м³	20 шт.
Доска 45х6000	0,071 м³	14 шт.

Необрезная доска : что это

Необрезная доска — это первые снятые со ствола доски. Ее Кромки не отторцованы и имеют обзол, что недопустимо для обрезной доски. У необрезной доски кора на боковых кромках. Первая, снятая со ствола доска имеет больше всего коры. Стандартная толщина необрезных досок 25, 40, 50 мм, а длина — 6 м. Необрезные доски самый дешевые из всех досок. Поэтому их используют для лесов, обшивки, обрешетки крыши, компонентов несущих конструкций, настилов, черновых полов, на дрова. Для того, чтобы необрезные доски не начали гнить с них нужно снять кору, просушить и обработать антисептиком.

alexmalyutin.ru

Количество досок в кубе: расчет, онлайн-калькулятор и готовые таблицы

Любые строительные работы с применением пиломатериала рано или поздно поставят перед вами вопрос – сколько досок определенного типоразмера будет содержать один куб. Облегчить задачу расчета, привести готовые таблицы-кубатурники, а также рассказать о существующих нюансах перевода кубометров в количество досок и наоборот мы и постараемся в данной статье.

Содержание: [Скрыть]

Порядок и методика расчета

Чтобы рассчитать, сколько досок будет в одном кубе, достаточно освежить в памяти знания из курса математики средней школы. Переходим к порядку расчета.

Исходные данные

В расчетах будем отталкиваться от размеров доски. Используется три значения: высота (толщина), ширина и длина. В обозначении сортамента они приводятся в таком же порядке, например 25×150×6000 и указываются в миллиметрах.

Важно! Перед началом расчета не забудьте перевести значения геометрических размеров в метры. Так как мы рассматриваем расчет для нахождения количества досок в 1 метре кубическом, значит и все исходные данные должны быть приведены к размеру в метрах.

Высота и ширина (сечение) обрезного пиломатериала регламентируются ГОСТ 24454-80 «Пиломатериалы хвойных пород. Размеры», хотя у продавцов они могут иметь и другие значения.

Отметим, что для расчетов пиломатериалов специального назначения, отличающихся от стандартной прямоугольной формы в поперечном сечении (к примеру, шпунтованной половой доски), значения размеров высоты и ширины следует принимать по лицевой, «рабочей» ширине поверхности.

Для длины обрезного пиломатериалы наиболее популярные на рынке предложения – это 4-х и 6-ти метровые доски.

Важно! Покупая необрезную доску неизвестных геометрических параметров, размеры её сечения для последующего расчета кубатуры лучше находить как среднее значение между высотой и шириной, измеренных с обеих сторон.

Расчет количества досок в кубе

Отталкиваться будем от простой геометрической формулы: объем равен произведению длин трех сторон. По ней, используя исходные данные, рассчитываем объем одной доски. Затем делим 1 на полученное значение и получаем итоговую цифру сколько досок содержится в кубе в штуках.

Символьной формулой расчет кубатуры доски можно записать так:

1 / (L*h*b) = N, где

h, b, L – высота, ширина и длина доски соответственно, м;

N – количество досок в 1 м3, штук.

Нужно понимать, что расчет по обозначенной формуле носит ориентировочный характер. Число может получиться и дробное, хотя при покупке вы заберете количество, кратное целому и округленное в меньшую сторону. Также производителем пиломатериала могут четко не соблюдаться номинальные значения геометрических размеров, и фактическое количество досок в одном кубе может составить как большее значение, так и меньшее от расчетного. Кроме того, не следует руководствоваться расчетом «впритык». Не весь купленный пиломатериал может оказаться пригодным к использованию, поэтому процентов 10-15 запаса по количеству, особенно при больших партиях закупки, следует закладывать на брак.

Важно! При покупке объема пиломатериала, превышающего 1 м3, требуйте расчета количества отпускаемой вам доски от всего объема по вышеприведенной формуле (подставляя вместо единицы в числителе нужный вам объем), а не по одному кубу с последующим округлением и умножением – недобросовестные продавцы на этом могут сэкономить.

Расчет покрытия в м2 одним кубометром доски

Данный расчет – частный случай, востребованный когда нужно знать, сколько квадратных метров способен покрыть один метр кубический пиломатериала, например, для половой доски или же стеновой вагонки.

Формула все также проста – нужно полученное по результатам прошлого расчета количество досок в кубе (округленное до целого числа) умножить на площадь одной доски (произведение длины на ширину). Выражаясь символьным языком, это выглядит следующим образом:

S = N * b * L, где

S – площадь в м2, «зашиваемая» 1 м3 доски.

Важно! Расчетное значение площади доски в одном кубометре также получается ориентировочной цифрой, которую, при закупке пиломатериала на необходимый метраж в «квадратах», следует брать с определенным запасом.

Калькуляторы кубатуры досок

Рассмотрев вышеприведенные формулы, в теории становится понятно, как посчитать кубатуру доски. Для повседневного использования и упрощения рутинного процесса на нашем сайте размещены калькуляторы, осуществляющие онлайн-расчет по различным критериям.

Калькулятор расчета количества досок в кубе

Данный калькулятор осуществляет расчет количества досок в штуках, содержащихся в заданном объеме пиломатериала в кубометрах. Чтобы рассчитать искомый показатель, необходимо ввести в соответствующие поля параметры одной доски (ширина, толщина, длина – в мм) и общий объем досок в м3.

Итоговый результат в штуках может иметь дробное значение, но продавцы пиломатериала, как правило, округляют расчетное количество досок в кубе до ближайшего меньшего целого числа, что также учитывает и наш онлайн-калькулятор.

Калькулятор расчета кубатуры досок по их количеству

Нижеприведенный калькулятор будет полезен, когда возникает задача перевести доски в кубы. В качестве исходных данных, как и для предыдущего онлайн-расчета, используется геометрические размеры одной доски в мм и общее количество досок в штуках, для которых нужно определить их кубатуру в м3.

Готовые таблицы количества досок в кубе

Несмотря на простоту формулы определения кубатуры пиломатериала и наличие доступных онлайн-калькуляторов, рассчитывать каждый раз сколько досок в кубе для разных размеров достаточно неудобно. Для избавления от этого рутинного процесса созданы уже готовые таблицы-кубатурники, которыми достаточно удобно пользоваться для быстрого определения количества штук пиломатериала в 1 м3.

Сколько 6-ти метровых досок в 1 кубе: таблица

Размеры доски, мм Количество в 1 кубе Площадь, покрываемая 1 м3 доски

Доска-«двадцатка» (толщина 20 мм)
20×100×6000	83 шт.	49,8 м2
20×120×6000	69 шт.	49,7 м2
20×150×6000	55 шт.	49,5 м2
20×180×6000	46 шт.	49,7 м2
20×200×6000	41 шт.	49,2 м2
20×250×6000	33 шт.	49,5 м2
Доска-«двадцатьпятка» (толщина 25 мм)
25×100×6000	66 шт.	39,6 м2
25×120×6000	55 шт.	39,6 м2
25×150×6000	44 шт.	39,6 м2
25×180×6000	37 шт.	40 м2
25×200×6000	33 шт.	39,6 м2
25×250×6000	26 шт.	39 м2
Доска-«тридцатка» (толщина 30 мм)
30×100×6000	55 шт.	33 м2
30×120×6000	46 шт.	33,1 м2
30×150×6000	37 шт.	33,3 м2
30×180×6000	30 шт.	32,4 м2
30×200×6000	27 шт.	32,4 м2
30×250×6000	22 шт.	33 м2
Доска-«тридцатидвушка» (толщина 32 мм)
32×100×6000	52 шт.	31,2 м2
32×120×6000	43 шт.	31 м2
32×150×6000	34 шт.	30,6 м2
32×180×6000	28 шт.	30,2 м2
32×200×6000	26 шт.	31,2 м2
32×250×6000	20 шт.	30 м2
Доска-«сороковка» (толщина 40 мм)
40×100×6000	41 шт.	24,6 м2
40×120×6000	34 шт.	24,5 м2
40×150×6000	27 шт.	24,3 м2
40×180×6000	23 шт.	24,8 м2
40×200×6000	20 шт.	24 м2
40×250×6000	16 шт.	24 м2
Доска-«пятидесятка» (толщина 50 мм)
50×100×6000	33 шт.	19,8 м2
50×120×6000	27 шт.	19,4 м2
50×150×6000	22 шт.	19,8 м2
50×180×6000	18 шт.	19,4 м2
50×200×6000	16 шт.	19,2 м2
50×250×6000	13 шт.	19,5 м2

Сколько 4-х метровых досок в 1 кубе: таблица

Размеры доски, мм Количество в 1 кубе Площадь, покрываемая 1 м3 доски

Доска-«двадцатка» (толщина 20 мм)
20×100×4000	125 шт.	50 м2
20×120×4000	104 шт.	49,9 м2
20×150×4000	83 шт.	49,8 м2
20×180×4000	69 шт.	49,7 м2
20×200×4000	62 шт.	49,6 м2
20×250×4000	50 шт.	50 м2
Доска-«двадцатьпятка» (толщина 25 мм)
25×100×4000	100 шт.	40 м2
25×120×4000	83 шт.	39,8 м2
25×150×4000	66 шт.	39,6 м2
25×180×4000	55 шт.	39,6 м2
25×200×4000	50 шт.	40 м2
25×250×4000	40 шт.	40 м2
Доска-«тридцатка» (толщина 30 мм)
30×100×4000	83 шт.	33,2 м2
30×120×4000	69 шт.	33,1 м2
30×150×4000	55 шт.	33 м2
30×180×4000	46 шт.	33,1 м2
30×200×4000	41 шт.	32,8 м2
30×250×4000	33 шт.	33 м2
Доска-«тридцатидвушка» (толщина 32 мм)
32×100×4000	78 шт.	31,2 м2
32×120×4000	65 шт.	31,2 м2
32×150×4000	52 шт.	31,2 м2
32×180×4000	43 шт.	31 м2
32×200×4000	39 шт.	31,2 м2
32×250×4000	31 шт.	31 м2
Доска-«сороковка» (толщина 40 мм)
40×100×4000	62 шт.	24,8 м2
40×120×4000	52 шт.	25 м2
40×150×4000	41 шт.	24,6 м2
40×180×4000	34 шт.	24,5 м2
40×200×4000	31 шт.	24,8 м2
40×250×4000	25 шт.	25 м2
Доска-«пятидесятка» (толщина 50 мм)
50×100×4000	50 шт.	20 м2
50×120×4000	41 шт.	19,7 м2
50×150×4000	33 шт.	19,8 м2
50×180×4000	27 шт.	19,4 м2
50×200×4000	25 шт.	20 м2
50×250×4000	20 шт.	20 м2

Таблица кубатуры необрезного пиломатериала

Составление готовой точной таблицы для такого рода изделий, как и точный расчет, затруднительны. Необрезной пиломатериал получают продольным распиливанием бревна на доски без дальнейшей их обработки по кромкам. В такой ситуации в зависимости от участка выпилки меняется и ширина полученной доски, постоянными остаются только длина и высота (толщина).

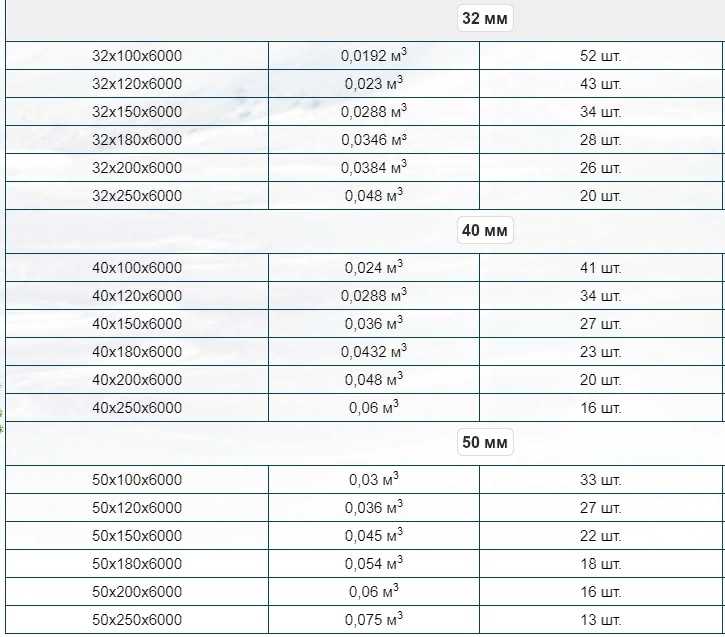
Чтобы хотя бы примерно представлять, сколько необрезной доски будет в одном кубе, мы приводим типовой вариант таблицы-кубатурника необрезного пиломатериала длиной 6 метров и стандартного ряда толщин 25, 40 и 50 мм:

Особенности практического применения расчета и таблиц

Следует понимать, что алгоритм расчета количества доски в кубе будет одинаков для пиломатериала с различными степенями осушки или же из различных пород древесины. Каких-то дополнительных ухищрений тут не требуется.

Также отметим, что табличные значения являются, хоть и с высокой степень точности, но все-таки ориентировочными данными. В действительности, при подсчете реального количества досок в кубе, многое будет зависеть от плотности укладки штабеля, ведь пиломатериал не прилегает друг к другу идеально плотно, как то подразумевает математическая модель расчета. Помните об этом, рассчитывайте по формулам или таблицам сколько кубов пиломатериала вам необходимо и рассматривайте приобретение расчетного количества с определенным запасом.

drevesina.info

Сколько штук досок в 1 кубе

Главная | Статьи | Сколько досок в 1 кубе

Для упрощения счета, мы подготовили для Вас сводную таблицу. Таблица позволяет сразу узнать, сколько досок в 1 кубе, не уделяя время расчетам. Чтобы Вам было удобно.

Сколько штук обрезной и строганной доски в 1 кубе таблица

Размеры, мм	Объём досок в 1 м3	Количество досок в м3	Количество досок в м2

20х100х6000	0,012 м3	83 шт.	50 м2
20х120х6000	0,0144 м3	69 шт.	50 м2
20х150х6000	0,018 м3	55 шт.	50 м2
20х180х6000	0,0216 м3	46 шт.	50 м2
20х200х6000	0,024 м3	41 шт.	50 м2
20х250х6000	0,03 м3	33 шт.	50 м2

25х100х6000	0,015 м3	67 шт.	40 м2
25х120х6000	0,018 м3	55 шт.	40 м2
25х150х6000	0,0225 м3	44 шт.	40 м2
25х180х6000	0,027 м3	37 шт.	40 м2
25х200х6000	0,03 м3	33 шт.	40 м2
25х250х6000	0,0375 м3	26 шт.	40 м2

30х100х6000	0,018 м3	55 шт.	33 м2
30х120х6000	0,0216 м3	46 шт.	33 м2
30х150х6000	0,027 м3	37 шт.	33 м2
30х180х6000	0,0324 м3	30 шт.	33 м2
30х200х6000	0,036 м3	27 шт.	33 м2
30х250х6000	0,045 м3	22 шт.	33 м2

32х100х6000	0,0192 м3	52 шт.	31 м2
32х120х6000	0,023 м3	43 шт.	31 м2
32х150х6000	0,0288 м3	34 шт.	31 м2
32х180х6000	0,0346 м³	28 шт.	31 м2
32х200х6000	0,0384 м3	26 шт.	31 м2
32х250х6000	0,048 м3	20 шт.	31 м2

40х100х6000	0,024 м3	41 шт.	25 м2
40х120х6000	0,0288 м3	34 шт.	25 м2
40х150х6000	0,036 м3	27 шт.	25 м2
40х180х6000	0,0432 м3	23 шт.	25 м2
40х200х6000	0,048 м3	20 шт.	25 м2
40х250х6000	0,06 м3	16 шт.	25 м2

50х100х6000	0,03 м3	33 шт.	20 м2
50х120х6000	0,036 м3	27 шт.	20 м2
50х150х6000	0,045 м3	22 шт.	20 м2
50х180х6000	0,054 м3	18 шт.	20 м2
50х200х6000	0,06 м3	16 шт.	20 м2
50х250х6000	0,075 м3	13 шт.	20 м2

Формулы расчета доски

Примеры расчета доски размером 20х100х6000 мм

Формула расчета объема доски:0,02 м · 0,1 м · 6 м = 0,012 м3

Формула расчета доски в кубе в штуках:1 м3 / 0,012 м3 = 83 шт./м3

Формула расчета доски в кубе в квадратах:1 м3 / 0,02 м = 50 м2/м3

Чтобы решить, сколько досок в 1 кубе, сначала нужно знать основные параметры приобретаемого материала – толщину, ширину и длину. Также можно делать расчет для досок размером 3 метра, 4 метра, 5 метров.

Страница содержит ответы на простые вопросы людей:

Сколько досок
Сколько кубов доски
Сколько штук досок
Досок в кубе
Сколько кубов в досках
Сколько штук в одном кубе
Сколько в кубе обрезной доски
Как подсчитать сколько досок в 1 кубе

Зачем считать, сколько досок в 1 кубе?

Всего две причины для того, чтобы произвести расчеты:

Вы узнаете общую цену всего объема бруса, нужного для вашего проекта. Достаточно знать цену за 1 доску и сколько всего штук (определяется расчетным путем или из нашей таблицы для стандартных размеров досок).
Вы подсчитаете общее число досок, нужное для осуществления вашего проекта. И сделать расчет можно, зная, сколько нужно кубов материала для работы, и определив количество штук досок в 1 кубе.

Но если боитесь сделать неправильные расчеты, позвоните по телефонам +7 (495) 775-83-74 или 8 (800) 775-83-74 и наши специалисты помогут разобраться с правильным подсчетом!

sbitsnab.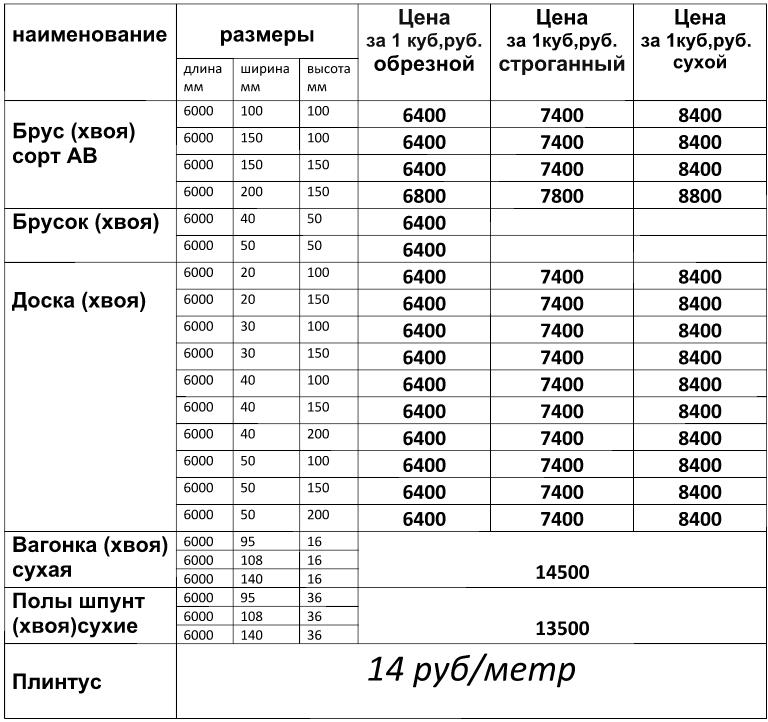 ru

Сколько досок в 1 кубе: расчет объема и веса обрезных, необрезных изделий

Все фото из статьи

Прежде чем приступить к любым строительным работам, необходимо выполнить проект и составить смету. Последняя подразумевает расчет материалов, причем, пиломатериалы всегда рассчитываются в кубах. Чтобы помочь в этом вопросе, далее мы рассмотрим, как посчитать количество досок в 1м3, а также приведем таблицу с их размерами и количеством в одном кубическом метре.

Рассчитанные по кубам доски

Общие сведения

Как правило, расчет досок, необходимых для выполнения тех или иных работ, у домашних мастеров не вызывает сложности. Но, как уже было сказано выше, этот материал продается на кубы, соответственно, прежде чем закупить его, необходимо перевести количество штук в объем.

Если посчитать обрезной материал своими руками еще не так сложно, благодаря правильной геометрии его формы, то узнать объем необрезного значительно сложней.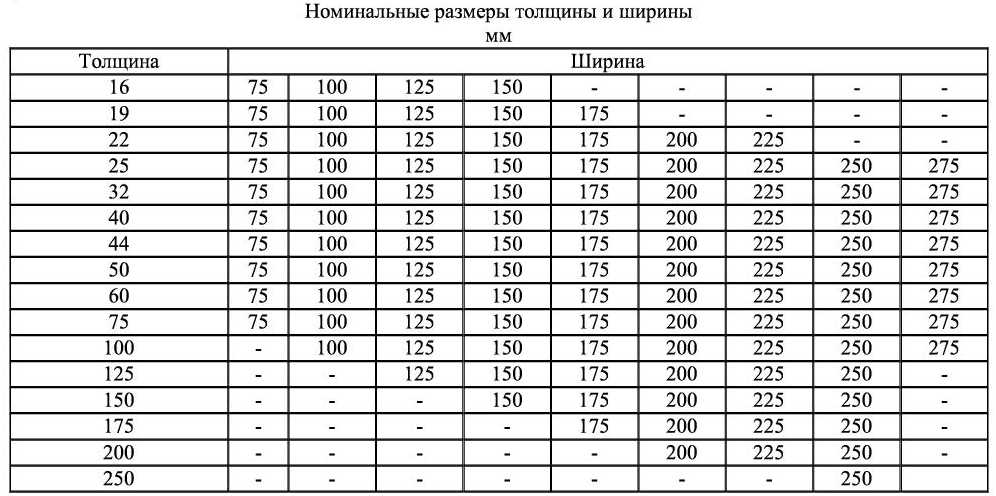 В данной статье мы ознакомимся с особенностями расчета для каждого типа пиломатериалов.

Обрезные дощечки

Рассчитываем объем

Обрезная

В качестве примера рассмотрим сколько нужно досок на пол в помещение площадью 20м2, если они имеют следующие параметры:

сечение – 150х30;
длина 6 метров.

Формула объема V=a*b*c

Инструкция по расчету выглядит так:

прежде всего узнаем количество досок, требующихся для обустройства деревянного пола. Для этого надо общую площадь разделить на площадь одной дощечки. Поэтому прежде всего узнаем площадь материала 0,15х6=0,9м2;
теперь можно посчитать его количество – 20/0,9=22,2~23 штуки. Конечно, материал надо приобретать с небольшим запасом, поэтому полученное значение увеличим до 25 штук;
далее нужно узнать объем одной дощечки, перемножив все ее параметры – 0,03х0,15х6=0,027 м3;
затем нужно узнать 1 куб досок – это сколько штук, поделив один куб на полученное ранее значение – 1/0,027=37 штук;
теперь осталось узнать необходимое количество пиломатериала в объеме. Для этого нужно выполнить следующее действие – 25/37=0,67 м3.

По этой схеме можно посчитать объем пиломатериала необходимого для любых типов строительных работ.

Обратите внимание! Если закупается сырое дерево, то потребуется гораздо больший его объем, так как в процессе высыхания оно уменьшится в размерах.

Теперь, когда известно количество пиломатериала в 1м3, не составит труда узнать и какова цена одной дощечки. Для этого стоимость куба нужно поделить на количество штук в метре кубическом.

Необрезной пиломатериал

Необрезная

Рассчитать объем необрезной доски несколько сложней:

Дело в том, что ее получают путем распиловки необработанного бревна. В результате она имеет неровные кромки, которые называются обзолом. Соответственно, ширина по всей длине может быть неодинаковой. Поэтому для расчета берется усредненное значение ширины;
Если же разбег ширины пласти слишком большой, дерево рассортировывается на несколько стопок, в которые укладываются схожие по длине и ширине дощечки;
Если же необходимо узнать объем, который требуется для обшивки поверхности, то следует измерить площадь этой поверхности, а затем умножить его на толщину материала. Кроме того, существуют и другие некоторые методы расчета, но описанные выше являются наиболее простыми и достаточно точными.

На фото — измерение ширины рулеткой

Совет! Из необрезной доски можно получить обрезную, удалив обзол, к примеру, при помощи циркулярной пилы для дерева. Выход обрезного материала из необрезного составляет 80 процентов.

Таблица

Как правило, пиломатериалы имеют стандартные размеры, соответственно, все их параметры известны. Поэтому, чтобы не тратить время на расчеты, можно воспользоваться параметрами, которые содержит таблица – сколько штук досок в 1 кубе:

Размер сечения, мм	Досок в 1 м3 при длине 6 м, шт.
50х250	13,3
50х200	16,6
50х150	22,2
50х100	33,3
50х50	66,6
40х200	20,8
40х150	27,7
40х100	41,6
25х200	33,3
25х150	44,4
25х100	66,6

Если необходимого размера сечения здесь нет, можно обратиться к справочной литературе, где содержатся более обширные данные.

Следует отметить, что таблица — сколько доски в 1 кубе подходит и для необрезного пиломатериала, единственное, как уже было сказано выше, следует ориентироваться на среднее значение ширины. Конечно, данные будут неточными, но, как правило, высокая точность при подобных подсчетах и не нужна.

Дубовое дерево является самыми тяжелыми

Вес

Нередко перед закупкой материала необходимо узнать его вес. Самостоятельно рассчитать этот параметр не получится, так как он зависит от плотности древесины и влажности. Поэтому ниже приведем таблицу с весом разных пород:

Порода древесины	Вес 1м3 при влажности 10%	Вес 1м3 при влажности 20%
Ель	440	460
Сосна	430	450
Осина	490	510
береза	630	650
Лиственница	660	690
Ясень	670	610
Дуб	680	720
Бук	670	690

Совет! Приобретать лучше сухое дерево, так как при самостоятельной сушке оно может растрескиваться и деформироваться. Соответственно, количество пригодного для использования материала уменьшится.

Оптимальная влажность составляет 8-12 процентов.

Зная, сколько весит 1м3 дерева, можно рассчитать количество машин, которые потребуются для транспортировки материала, и, таким образом, посчитать расходы на доставку.

Вывод

Узнать основные параметры досок, такие как объем и вес, можно из справочной литературы. Однако, таблица сколько шт досок в 1 кубе не всегда имеется под рукой, поэтому иногда приходится выполнять расчет самостоятельно. Заключается он в нескольких простых математических действиях, из которых составлена инструкция.

Из видео в этой статье можно ознакомиться с дополнительной информацией. Если после прочтения материала у вас появились вопросы, вы можете оставить их в комментариях, и мы с радостью на них ответим.

rubankom.com

Смотрите также

Жидкие обои с рисунком в интерьере фото
Как поставить в квартире счетчик на газ
Гаечный ключ двухсторонний
Опалубка для монолитного строительства своими руками
Сколько необрезной доски в кубе таблица
Жидкие обои с рисунком в интерьере фото
Аква лаки по дереву
Опалубка для монолитного строительства своими руками
Палитры сочетания цветов пастельные
Аква лаки по дереву
Сколько в кубе бруса 100х150

Сколько штук теса в одном кубе 6 метра

Главная » Автолюбителю

Автор Сфера закона На чтение 6 мин Просмотров 6 Опубликовано 25 августа 2022

Содержание

Сколько досок в 1 кубе: таблица 3 и 6 метров

Таблица соответствия на 6 метров
Сколько штук досок в 1 кубе
Сколько штук обрезной и строганной доски в 1 кубе таблица
Формулы расчета доски
Страница содержит ответы на простые вопросы людей:
Зачем считать, сколько досок в 1 кубе?
Сколько досок в кубе: готовые таблицы-кубатурники
Сколько 4-х метровых досок в 1 кубе: таблица
Как заказать?

Сколько досок в 1 кубе: таблица 3 и 6 метров

Чтобы узнать количество разных по длине досок в 1 кубе, можно применить таблицу или провести расчёт самостоятельно. Реализация продукции происходит в кубических метрах, при этом указывают следующие параметры:

Длина — метр или миллиметр.
Ширина и толщина — миллиметр.

Все единицы измерения переводим в метры.

Расчёт: 1 м 3 , разделить на объём доски, он будет — 0,045 м 3 , получим — 22,2 шт.

Получилось не целое число, но при покупке объём будет соблюдаться. Для реализации предлагается пиломатериал больше по длине, на несколько сантиметров. Чтобы не возникло недостатка, который может получиться за счёт ширины поперечного распила.

Ниже представлена таблица, из которой видно, сколько досок в 1 кубе по 6 метров.

Таблица соответствия на 6 метров

Если нужны доски диной 3 метра одинаковой толщины, то количество следует умножить на два.

Ниже представлена таблица, из которой видно, сколько досок в 1 кубе по 3 метра.

Источник

Сколько штук досок в 1 кубе

Сколько штук обрезной и строганной доски в 1 кубе таблица

Размер сечения, мм	Длина, м	Количество досок в 1 кубе
25х100	6	66,67
25х150	6	44,44
40х100	6	41,67
50х100	6	33,33
40х150	6	27,78
50х150	6	22,22
50х200	6	16,67

Размеры, мм	Объём досок в 1 м 3	Количество досок в м 3	Количество досок в м 2

20х100х6000	0,012 м 3	83 шт.	50 м 2
20х120х6000	0,0144 м 3	69 шт.	50 м 2
20х150х6000	0,018 м 3	55 шт.	50 м 2
20х180х6000	0,0216 м 3	46 шт.	50 м 2
20х200х6000	0,024 м 3	41 шт.	50 м 2
20х250х6000	0,03 м 3	33 шт.	50 м 2

25х100х6000	0,015 м 3	67 шт.	40 м 2
25х120х6000	0,018 м 3	55 шт.	40 м 2
25х150х6000	0,0225 м 3	44 шт.	40 м 2
25х180х6000	0,027 м 3	37 шт.	40 м 2
25х200х6000	0,03 м 3	33 шт.	40 м 2
25х250х6000	0,0375 м 3	26 шт.	40 м 2

30х100х6000	0,018 м 3	55 шт.	33 м 2
30х120х6000	0,0216 м 3	46 шт.	33 м 2
30х150х6000	0,027 м 3	37 шт.	33 м 2
30х180х6000	0,0324 м 3	30 шт.	33 м 2
30х200х6000	0,036 м 3	27 шт.	33 м 2
30х250х6000	0,045 м 3	22 шт.	33 м 2

32х100х6000	0,0192 м 3	52 шт.	31 м 2
32х120х6000	0,023 м 3	43 шт.	31 м 2
32х150х6000	0,0288 м 3	34 шт.	31 м 2
32х180х6000	0,0346 м³	28 шт.	31 м 2
32х200х6000	0,0384 м 3	26 шт.	31 м 2
32х250х6000	0,048 м 3	20 шт.	31 м 2

40х100х6000	0,024 м 3	41 шт.	25 м 2
40х120х6000	0,0288 м 3	34 шт.	25 м 2
40х150х6000	0,036 м 3	27 шт.	25 м 2
40х180х6000	0,0432 м 3	23 шт.	25 м 2
40х200х6000	0,048 м 3	20 шт.	25 м 2
40х250х6000	0,06 м 3	16 шт.	25 м 2

50х100х6000	0,03 м 3	33 шт.	20 м 2
50х120х6000	0,036 м 3	27 шт.	20 м 2
50х150х6000	0,045 м 3	22 шт.	20 м 2
50х180х6000	0,054 м 3	18 шт.	20 м 2
50х200х6000	0,06 м 3	16 шт.	20 м 2
50х250х6000	0,075 м 3	13 шт.	20 м 2

Формулы расчета доски

Примеры расчета доски размером 20х100х6000 мм

Формула расчета объема доски:
0,02 м · 0,1 м · 6 м = 0,012 м 3

Формула расчета доски в кубе в штуках:
1 м3 / 0,012 м 3 = 83 шт.

/м 3

Формула расчета доски в кубе в квадратах:
1 м 3 / 0,02 м = 50 м 2 /м 3

Страница содержит ответы на простые вопросы людей:

Сколько досок
Сколько кубов доски
Сколько штук досок
Досок в кубе
Сколько кубов в досках
Сколько штук в одном кубе
Сколько в кубе обрезной доски
Как подсчитать сколько досок в 1 кубе

Зачем считать, сколько досок в 1 кубе?

Всего две причины для того, чтобы произвести расчеты:

Вы узнаете общую цену всего объема бруса, нужного для вашего проекта. Достаточно знать цену за 1 доску и сколько всего штук (определяется расчетным путем или из нашей таблицы для стандартных размеров досок).
Вы подсчитаете общее число досок, нужное для осуществления вашего проекта. И сделать расчет можно, зная, сколько нужно кубов материала для работы, и определив количество штук досок в 1 кубе.

Источник

Сколько досок в кубе: готовые таблицы-кубатурники

Количество штук доски в одном кубе зависит от размеров доски . Необходимое количество обрезных досок и сколько квадратных метров покрывает 1 кубический метр доски, можно посчитать, используя таблицы пилорамы “78 Досок”.

Сколько 6-ти метровых досок в 1 кубе: таблица

Размеры доски, мм	Количество в 1 кубе	Площадь, покрываемая 1 м 3 доски
Сколько досок толщиной 20мм в кубе («двадцатка»)
20×100×6000	83 шт.	49,8 м 2
20×120×6000	69 шт.	49,7 м 2
20×150×6000	55 шт.	49,5 м 2
20×180×6000	46 шт.	49,7 м 2
20×200×6000	41 шт.	49,2 м 2
20×250×6000	33 шт.	49,5 м 2
Сколько досок толщиной 25 мм в кубе («двадцатьпятка»)
25×100×6000	66 шт.	39,6 м 2
25×120×6000	55 шт.	39,6 м 2
25×150×6000	44 шт.	39,6 м 2
25×180×6000	37 шт.	40 м 2
25×200×6000	33 шт.	39,6 м 2
25×250×6000	26 шт.	39 м 2
Сколько досок толщиной 30 мм в кубе («тридцатка»)
30×100×6000	55 шт.	33 м 2
30×120×6000	46 шт.	33,1 м 2
30×150×6000	37 шт.	33,3 м 2
30×180×6000	30 шт.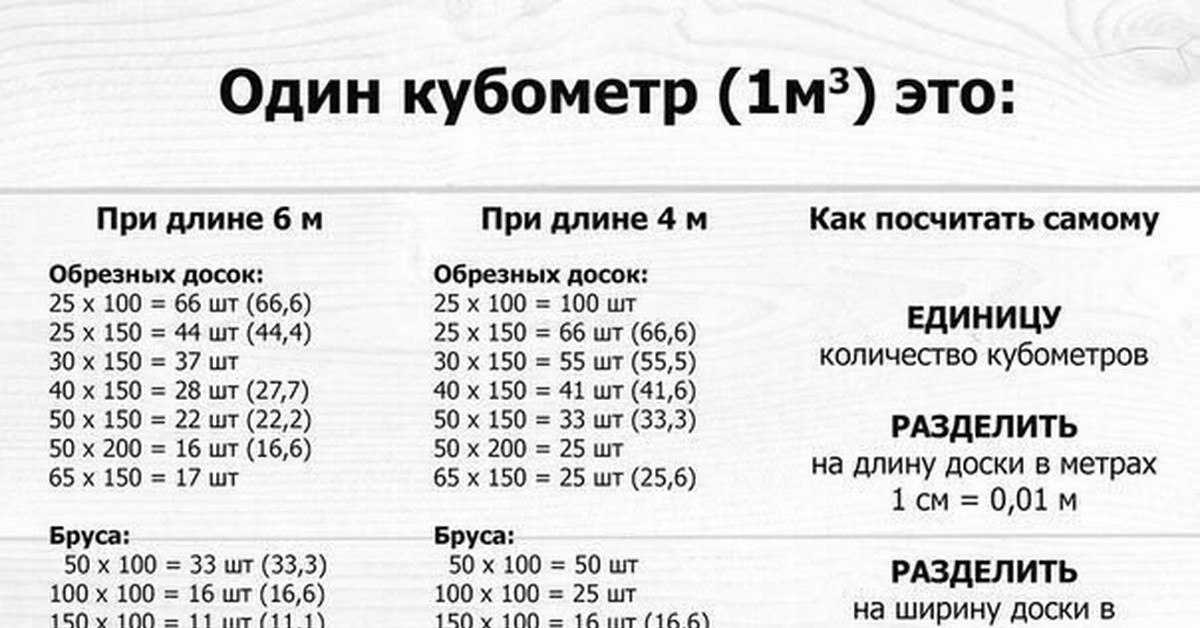	32,4 м 2
30×200×6000	27 шт.	32,4 м 2
30×250×6000	22 шт.	33 м 2
Сколько досок толщиной 32 мм в кубе («тридцатидвушка»)
32×100×6000	52 шт.	31,2 м 2
32×120×6000	43 шт.	31 м 2
32×150×6000	34 шт.	30,6 м 2
32×180×6000	28 шт.	30,2 м 2
32×200×6000	26 шт.	31,2 м 2
32×250×6000	20 шт.	30 м 2
Сколько досок толщиной 40 мм в кубе («сороковка»)
40×100×6000	41 шт.	24,6 м 2
40×120×6000	34 шт.	24,5 м 2
40×150×6000	27 шт.	24,3 м 2
40×180×6000	23 шт.	24,8 м 2
40×200×6000	20 шт.	24 м 2
40×250×6000	16 шт.	24 м 2
Сколько досок толщиной 40 мм в кубе («пятидесятка»)
50×100×6000	33 шт.	19,8 м 2
50×120×6000	27 шт.	19,4 м 2
50×150×6000	22 шт.	19,8 м 2
50×180×6000	18 шт.	19,4 м 2
50×200×6000	16 шт.	19,2 м 2
50×250×6000	13 шт.	19,5 м 2

Сколько 4-х метровых досок в 1 кубе: таблица

Размеры доски, мм	Количество в 1 кубе	Площадь, покрываемая 1 м 3 доски
Доска-«двадцатка» (толщина 20 мм)
20×100×4000	125 шт.	50 м 2
20×120×4000	104 шт.	49,9 м 2
20×150×4000	83 шт.	49,8 м 2
20×180×4000	69 шт.	49,7 м 2
20×200×4000	62 шт.	49,6 м 2
20×250×4000	50 шт.	50 м 2
Доска-«двадцатьпятка» (толщина 25 мм)
25×100×4000	100 шт.	40 м 2
25×120×4000	83 шт.	39,8 м 2
25×150×4000	66 шт.	39,6 м 2
25×180×4000	55 шт.	39,6 м 2
25×200×4000	50 шт.	40 м 2
25×250×4000	40 шт.	40 м 2
Доска-«тридцатка» (толщина 30 мм)
30×100×4000	83 шт.	33,2 м 2
30×120×4000	69 шт.	33,1 м 2
30×150×4000	55 шт.	33 м 2
30×180×4000	46 шт.	33,1 м 2
30×200×4000	41 шт.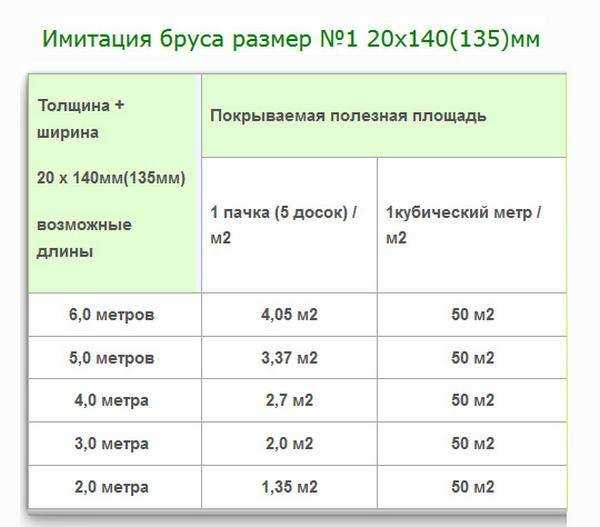	32,8 м 2
30×250×4000	33 шт.	33 м 2
Доска-«тридцатидвушка» (толщина 32 мм)
32×100×4000	78 шт.	31,2 м 2
32×120×4000	65 шт.	31,2 м 2
32×150×4000	52 шт.	31,2 м 2
32×180×4000	43 шт.	31 м 2
32×200×4000	39 шт.	31,2 м 2
32×250×4000	31 шт.	31 м 2
Доска-«сороковка» (толщина 40 мм)
40×100×4000	62 шт.	24,8 м 2
40×120×4000	52 шт.	25 м 2
40×150×4000	41 шт.	24,6 м 2
40×180×4000	34 шт.	24,5 м 2
40×200×4000	31 шт.	24,8 м 2
40×250×4000	25 шт.	25 м 2
Доска-«пятидесятка» (толщина 50 мм)
50×100×4000	50 шт.	20 м 2
50×120×4000	41 шт.	19,7 м 2
50×150×4000	33 шт.	19,8 м 2
50×180×4000	27 шт.	19,4 м 2
50×200×4000	25 шт.	20 м 2
50×250×4000	20 шт.	20 м 2

Узнать цены на пиломатериалы нашей пилорамы “78 Досок” в Яльгелево с доставкой по Санкт-Петербурге с Ленинградской области можно в разделе “ЦЕНЫ“

Как заказать?

Сделать заказ можно по телефону: +7(812)984-78-78

Источник

Сколько досок в 1 кубе? таблица, количество штук обрезной и необрезной досок в 1 м3. как посчитать кубатуру на калькуляторе? формула расчета

Сколько весит куб разных досок?

Приведем справочные данные для некоторых пород, которые помогут определиться, сколько весит куб разных досок.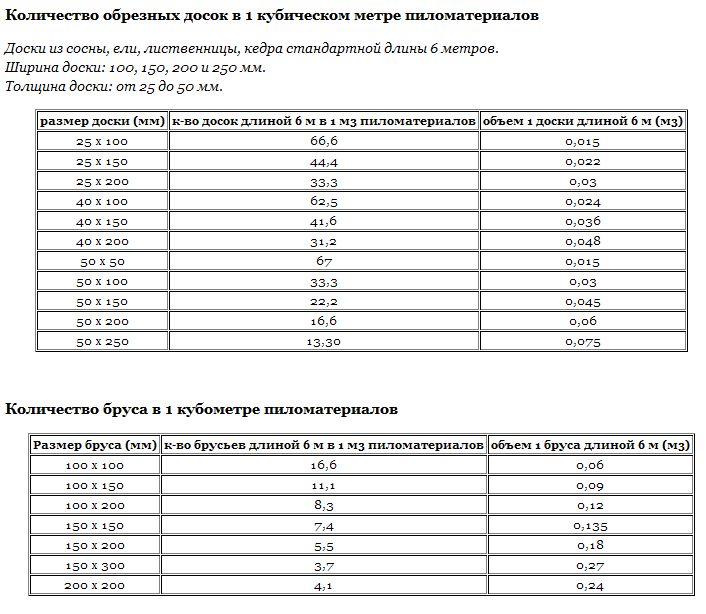

По породе

В зависимости от того, каковы плотность и вес куба разной древесины 12% влажности (все физико-технические свойства по ГОСТ определяют для этого уровня), все породы можно разделить на 3 класса.

Легкие – до 540 кг. Это большинство хвойных пород, в том числе ель, сосна обыкновенная, пихта, кедр. Из лиственных – орех, вишня, тополь, липа, ольха, осина.
Средней плотности – от 540 до 740 кг. К этой категории относятся ильм, береза повислая и пушистая, клен, ясень, яблоня, вяз.
Тяжелые – более 740 кг. Это дуб, венге, железная береза, граб, акация, самшит.

От плотности и веса во многом зависят свойства материалов и, следовательно, круг задач, для которых они лучше всего подходят.

Доски из твердых пород используют там, где требуется повышенная прочность: создание несущих перекрытий, полов, лестниц, массивной мебели, обшивки влажных помещений. Благодаря плотной структуре такие доски не только очень надежны, но и имеют благородный, эстетичный вид.
Доски из пород средней плотности и легкие доски хвойных пород востребованы для отделочных работ и изготовления мебели. Они не слишком тяжелые, но довольно прочные, обладают большей гибкостью, чем доски тяжелых пород. Это удачный вариант по соотношению цена/качество.
Доска из легких пород благодаря своей мягкой и податливой текстуре проста в обработке, поэтому она хорошо подходит для декоративной отделки и резьбы по дереву.

По влажности

Чтобы понять, насколько сильно вес зависит от влажности, рассмотрим, сколько в среднем весит куб древесины разных пород разной степени просушки. Древесина естественной влажности:

мягких лиственных пород (осина, липа, тополь, ольха) – 800 кг;
хвойных пород (сосна, ель, пихта) – 800 кг;
лиственных пород средней твердости (береза, яблоня, ясень) и лиственница – 900 кг;
твердых лиственных (дуб, акация) – 1000 кг.

Обрезная доска воздушно-сухой влажности:

мягких лиственных пород – 550 кг;
хвойных пород – 500 кг;
лиственных пород средней твердости – 650 кг;
твердых лиственных пород – 750 кг.

Сырая обрезная доска:

мягких лиственных пород – 550 кг;
хвойных пород – 500 кг;
лиственных пород средней твердости – 650 кг;
твердых лиственных пород – 750 кг.

Сухая (мебельная) обрезная доска:

мягких лиственных пород – 500 кг;
хвойных пород – 450 кг;
лиственных пород средней твердости – 600 кг;
твердых лиственных пород – 700 кг.

Средними значениями можно воспользоваться для предварительных расчетов. При этом нужно учитывать некоторые нюансы.

Фактический вес кубометра обрезной доски будет на 1–3% меньше табличного. Это связано с тем, что хотя благодаря правильной форме такие доски ровно укладываются в штабеля, но все же их невозможно подогнать настолько плотно, чтобы они весили как целый куб дерева.
Вес необрезной доски будет на 20–30% меньше, чем вес обрезной доски. Эта разница объясняется весом незаполненной скошенной кромки.
Ближе всего к табличным значениям удельной плотности будут параметры строганной доски.

Особенности и характеристики

Деревянные доски 50х200х6000 миллиметров довольно часто применяются в индивидуальном строительстве. Они обладают неплохими показателями прочности. Такие пиломатериалы позволяют возводить надежные конструкции самого разного типа.

Эти доски также могут похвастаться хорошими теплоизоляционными свойствами, поэтому их нередко используют и при создании жилых сооружений. Чаще всего данные материалы во время производства проходят тщательную сушку в камерном оборудовании. Изделия, обработанные таким образом, отличаются большей долговечностью и стойкостью, именно их используют для строительства прочных и надежных конструкций.

Данные образцы используют в строительстве гораздо реже, потому что они не могут похвастаться такой прочностью и долговечностью, как предыдущий вариант.

Все эти модели при производстве пропитываются особыми защитными веществами, которые предотвратят образование гниющих участков и плесени. Также они препятствуют действиям вредоносных насекомых. Древесина отдельно обрабатывается и антисептическими компонентами.

Какими гвоздями прибивать?

Независимо от того, какой крепёж вы используете – гвозди или саморезы, доску в каждом месте фиксации на балках или лагах необходимо засверлить сверлом, диаметр которого приблизительно равен диаметру гвоздя или самореза. Например, когда диаметр рабочей части гвоздя равен 5 миллиметрам, то сверло для предварительного засверливания необходимо брать на миллиметр меньше — в данном случае это 4 мм.

Дело в том, что если прибить доску гвоздём без предварительного засверливания, то она треснет вдоль — в окрестностях забиваемого гвоздя. Получившаяся трещина примет неровные очертания, что окончательно испортит внешний вид доски. Аналогичный эффект даст и саморез похожего диаметра — его винтовая канавка разопрёт деревоматериал в обе стороны.

Длина гвоздя (или самореза) определяется в основном толщиной основы (балки).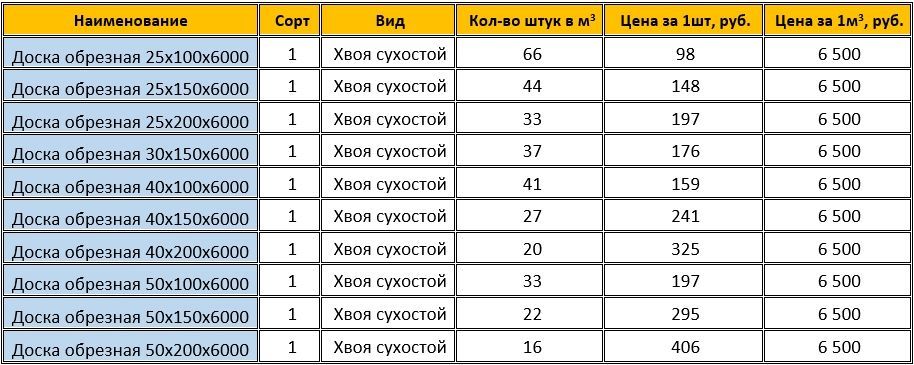 К 5 сантиметрам прибавляют, например, 8 см, когда балка представляет собой брус со стороной поперечного сечения в 10 см (или несущей основой выступает бревно с таким же диаметром). Конечная длина гвоздя или шурупа в этом случае — 13 см. Цель тщательного подбора гвоздя (или самореза), а также засверливающего сверла — не разрушить основание, на которое в ряд укладываются «пятидесятки».

Если лаги уложены на черновой (бетонный) пол в комнате или в ином помещении, вначале их аналогично прикрепляют саморезами или анкерными болтами по бетону, предварительно засверлив под них отверстия. Далее, зафиксировав эти балки, проверяют, чтобы потайные головки саморезов (или болтов) нигде не выступали. Черновой пол и лаги покрывают антисептической пропиткой. Затем на них укладывают сами доски. Полученный пол покрывают огнестойкой пропиткой и прокрашивают лаком или краской.

Какими бывают доски 50 мм и сколько их в 1 кубе, смотрите в видео ниже.

Готовые таблицы количества досок в кубе

Сколько 6-ти метровых досок в 1 кубе: таблица

Размеры доски, мм	Количество в 1 кубе	Площадь, покрываемая 1 м3 доски
Доска-«двадцатка» (толщина 20 мм)
20×100×6000	83 шт.	49,8 м2
20×120×6000	69 шт.	49,7 м2
20×150×6000	55 шт.	49,5 м2
20×180×6000	46 шт.	49,7 м2
20×200×6000	41 шт.	49,2 м2
20×250×6000	33 шт.	49,5 м2
Доска-«двадцатьпятка» (толщина 25 мм)
25×100×6000	66 шт.	39,6 м2
25×120×6000	55 шт.	39,6 м2
25×150×6000	44 шт.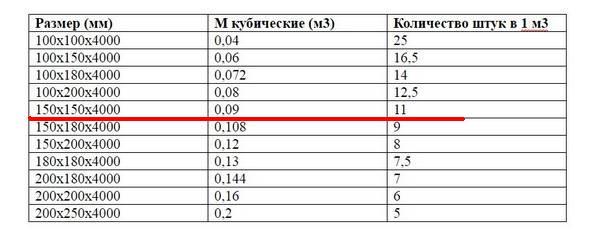	39,6 м2
25×180×6000	37 шт.	40 м2
25×200×6000	33 шт.	39,6 м2
25×250×6000	26 шт.	39 м2
Доска-«тридцатка» (толщина 30 мм)
30×100×6000	55 шт.	33 м2
30×120×6000	46 шт.	33,1 м2
30×150×6000	37 шт.	33,3 м2
30×180×6000	30 шт.	32,4 м2
30×200×6000	27 шт.	32,4 м2
30×250×6000	22 шт.	33 м2
Доска-«тридцатидвушка» (толщина 32 мм)
32×100×6000	52 шт.	31,2 м2
32×120×6000	43 шт.	31 м2
32×150×6000	34 шт.	30,6 м2
32×180×6000	28 шт.	30,2 м2
32×200×6000	26 шт.	31,2 м2
32×250×6000	20 шт.	30 м2
Доска-«сороковка» (толщина 40 мм)
40×100×6000	41 шт.	24,6 м2
40×120×6000	34 шт.	24,5 м2
40×150×6000	27 шт.	24,3 м2
40×180×6000	23 шт.	24,8 м2
40×200×6000	20 шт.	24 м2
40×250×6000	16 шт.	24 м2
Доска-«пятидесятка» (толщина 50 мм)
50×100×6000	33 шт.	19,8 м2
50×120×6000	27 шт.	19,4 м2
50×150×6000	22 шт.	19,8 м2
50×180×6000	18 шт.	19,4 м2
50×200×6000	16 шт.	19,2 м2
50×250×6000	13 шт.	19,5 м2

Сколько 4-х метровых досок в 1 кубе: таблица

Размеры доски, мм	Количество в 1 кубе	Площадь, покрываемая 1 м3 доски
Доска-«двадцатка» (толщина 20 мм)
20×100×4000	125 шт.	50 м2
20×120×4000	104 шт.	49,9 м2
20×150×4000	83 шт.	49,8 м2
20×180×4000	69 шт.	49,7 м2
20×200×4000	62 шт.	49,6 м2
20×250×4000	50 шт.	50 м2
Доска-«двадцатьпятка» (толщина 25 мм)
25×100×4000	100 шт.	40 м2
25×120×4000	83 шт.	39,8 м2
25×150×4000	66 шт.	39,6 м2
25×180×4000	55 шт.	39,6 м2
25×200×4000	50 шт.	40 м2
25×250×4000	40 шт.	40 м2
Доска-«тридцатка» (толщина 30 мм)
30×100×4000	83 шт.	33,2 м2
30×120×4000	69 шт.	33,1 м2
30×150×4000	55 шт.	33 м2
30×180×4000	46 шт.	33,1 м2
30×200×4000	41 шт.	32,8 м2
30×250×4000	33 шт.	33 м2
Доска-«тридцатидвушка» (толщина 32 мм)
32×100×4000	78 шт.	31,2 м2
32×120×4000	65 шт.	31,2 м2
32×150×4000	52 шт.	31,2 м2
32×180×4000	43 шт.	31 м2
32×200×4000	39 шт.	31,2 м2
32×250×4000	31 шт.	31 м2
Доска-«сороковка» (толщина 40 мм)
40×100×4000	62 шт.	24,8 м2
40×120×4000	52 шт.	25 м2
40×150×4000	41 шт.	24,6 м2
40×180×4000	34 шт.	24,5 м2
40×200×4000	31 шт.	24,8 м2
40×250×4000	25 шт.	25 м2
Доска-«пятидесятка» (толщина 50 мм)
50×100×4000	50 шт.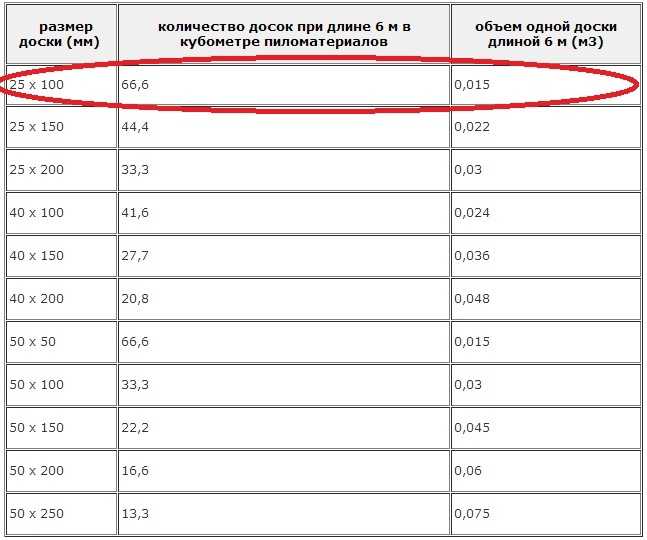	20 м2
50×120×4000	41 шт.	19,7 м2
50×150×4000	33 шт.	19,8 м2
50×180×4000	27 шт.	19,4 м2
50×200×4000	25 шт.	20 м2
50×250×4000	20 шт.	20 м2

Таблица кубатуры необрезного пиломатериала

Возможные ошибки

Ошибки в исчислении могут быть следующими:

взят не тот номинал среза доски;
не учтена требуемая длина экземпляра продукции;
выбрана не обрезная, а скажем, шпунтованная или не подвергавшаяся обрезанию по боковинам доска;
миллиметры, сантиметры не переведены в метры изначально, перед расчётом.

Все эти ошибки – следствие спешки и невнимательности. Это чревато как недостачей оплаченного и подвезённого пильного леса (тёса), так и его перерасходом и возникшей переплатой. Во втором случае пользователь ищет, кому бы продать остатки древесины, нужды в которой больше нет – стройка, отделка и изготовление мебели окончились, а реконструкции нет и не предвидится в ближайшие, скажем, лет двадцать-тридцать.

Сколько в кубе разных необрезных досок?

Перед реальным подсчётом необрезная доска не должна укладываться хаотично. Даже когда заготовки лежат плоскими сторонами и не параллельны друг другу — не прилегают, а могут располагаться перпендикулярно, воздушные зазоры в штабеле делаются минимальными. Предельный коэффициент воздушного пространства в необрезной доске не должен превышать 9%. Если он превысил этот уровень, то заготовки оказались не вполне похожими. Обнаружив это несоответствие, менеджер или завскладом даст указание грузчикам перепроверить штабель. Те удалят из него заготовки, отличающиеся от предельного допуска по размерам. Дело в том, что клиенты платят за дерево, а не за воздух.

Имея ограниченное количество отдаваемого для штабеля пространства — например, всё тот же 1 м3, 6-метровые доски не должны различаться по средней ширине. Например, нельзя в один штабель необрезных заготовок поместить экземпляры длиной 4 и 6 м — равно как и шириной 20-30 и 40-50 см, а также толщиной в 2,5 и 3 см. Последняя берётся из таблицы номиналов, имеющейся в каталоге склада или лесобазы, где приобретается необрезной материал.

В качестве примера — необрезные заготовки размером 30х150х6000 и 50х150х6000. Они часто присутствуют в каталогах большинства лесозаготовительных складов. Простой расчёт по упрощённой формуле, без необходимости повторно мерить каждый экземпляр в штабеле, выглядит следующим образом:

логично предположить, что допуск ширины – 145-155 мм в обоих случаях. объём доски равен 0,027 и 0,045 м3, соответственно;
количество целых заготовок на куб — 22 и 37 целых штук;
расположив их штабельно — по кубометру — получаем с учётом воздушного пространства, не закрытого древесиной, 20 и 33 шт. в худшем случае (с учётом 9% поправок на воздух).

Формулы расчета

Кубический метр – стандартная единица, принятая всеми отечественными и зарубежными производителями. Нередко используется также термин «погонаж» – общая длина всех досок.

Количество досок в кубе определяется простым расчетом. Вычисляют объем одного элемента – перемножают ширину, длину и толщину. А затем делят 1 м³ на полученный объем. Например:

пусть размеры составляют 25*100*6000 мм – один из самых популярных вариантов;
объем 1 такой доски будет составлять 0,015 м³;
количество в 1 кубе составляет 66,6 штук.

Поскольку строителю чаще нужно купить не 1 куб дюймовки, а необходимое число изделий, производят обратные вычисления. Рассчитывают кубатуру объема, который требуется для возведения здания или ограды. Для этого находят объем доски и умножают на необходимое число. Последний показатель обычно узнают, разделив площадь поверхности на площадь доски.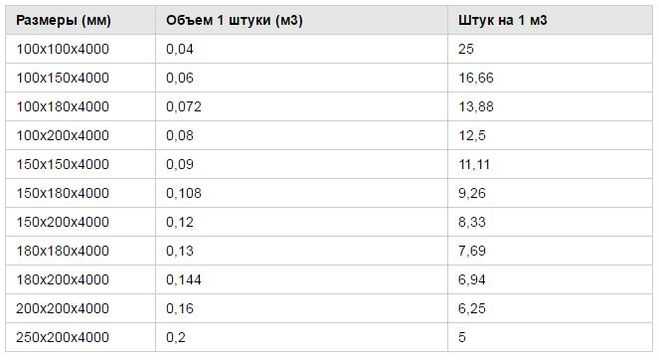 Затем умножают объем 1 элемента на нужное число. В итоге получают кубатуру – точный объем древесины, необходимый для строительства.

Что нужно учитывать при расчёте объёма?

Когда речь заходит о том, сколько весит конкретная порода дерева в кубометре, например, шпунтованной доски, то учитывают не только плотность той же лиственницы или сосны и степень просушки древесины

Не менее важно высчитать, сколько досок в кубометре этого же дерева – потребитель предпочитает знать заранее, с чем он столкнётся. Мало заказать и оплатить партию дерева – заказчику интересно будет выяснить, скольких человек нужно привлечь на разгрузку досок, как много времени займёт этот процесс, и каким образом сам клиент организует временное хранение заказанного деревоматериала, прежде чем тот весь уйдёт в предстоящее дело

Для определения количества досок в кубометре используется простая формула, известная с начальных классов школы – «куб» делят на объём пространства, занимаемый одной доской. А чтобы вычислить объём доски, её протяжённость умножают на площадь сечения – произведение толщины на ширину.

Но если с обрезной доской расчёт прост и ясен, то необрезная вносит некоторые коррективы. Необрезная доска – элемент, боковины которого по длине не выравнивались на пилораме при заготовке данной разновидности продукции. Она может быть уложена немного нестандартно за счёт перепадов ширины – в том числе и «валетом» – разных сторон. Так как распущенный на доски ствол сосны, лиственницы или иного древовидного сорта имеет переменную толщину от прикорневой зоны до вершины, за основу перерасчёта берётся среднее его значение по ширине. Необрезная доска и горбыль (поверхностный слой, имеющий одну округлую сторону по всей длине) отсортировываются в отдельные партии. Так как длина и толщина необрезной доски одинаковы, а ширина значительно разнится, то распущенная необрезанная продукция также предварительно сортируется по разной толщине, потому что полоса, прошедшая по центру сердцевины, окажется значительно шире, чем аналогичная часть, не затронувшая эту сердцевину вообще.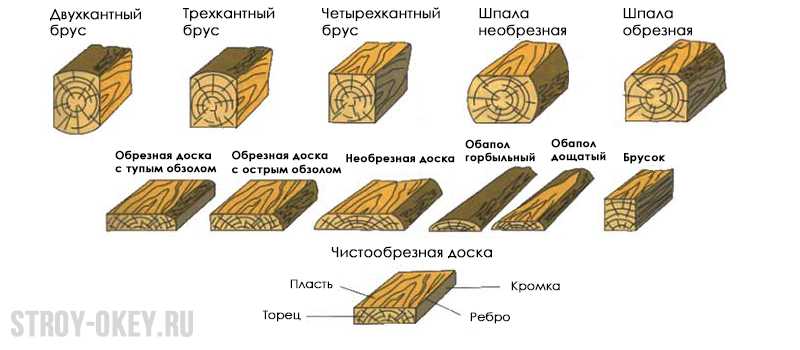

Для предельно точного подсчёта количества необрезной доски применяется следующий метод:

если на конце ширина доски составила 20 см, а в начале (у основания) – 24, то среднее значение выбирается равным 22;
подобные по ширине доски раскладываются таким образом, чтобы изменение ширины не превышало 10 см;
длина досок должна сходиться один в один;
используя рулеточную или «угольниковую» линейку, вымеряют высоту всей стопки досок;
вымеряется ширина досок по середине;
результат умножается на нечто среднее между поправочными значениями от 0,07 до 0,09.

Сколько Досок 40х150х6000 в 1 Кубе

Быстрая навигация по статье (содержание)

Определяем Сколько Досок 40х150х6000 в 1 Кубе Дерева
Как рассчитывается доска на практике?
Кубатурник досок таблица:

📝 Многие строительные материалы отпускаются в кубометрах.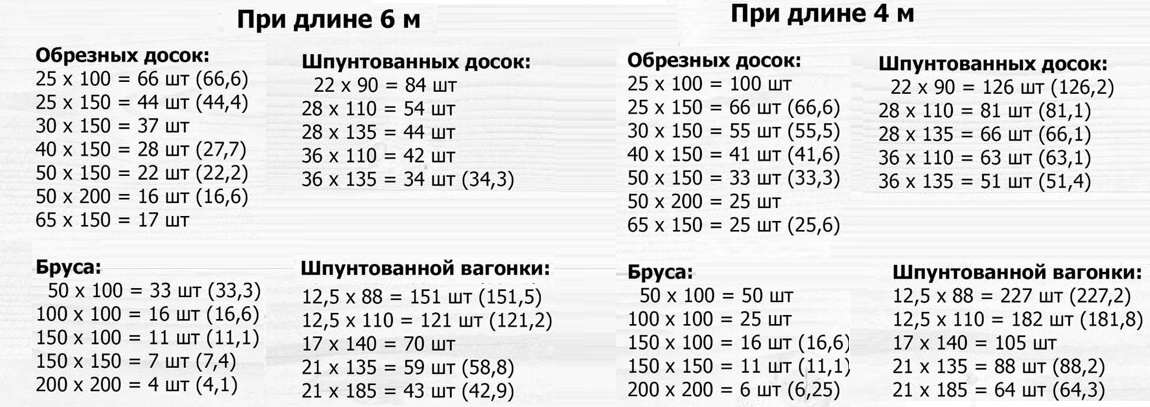 Но потребителей часто интересует количество изделий, приобретаемых кубометрами, в штуках. Как это делается, в этой статье будет рассказано сколько в кубе досок 40х150х6000 мм (толщина — ширина — длина).

Кубометр: что это и почему выбран он

Кубометр (1 м³) — объем правильного многогранника с квадратными гранями, все ребра которого равны одному метру. Для определения объёма достаточно знать длину, высоту и ширину ёмкости (стопки), измеренные в метрах (м), сантиметрах (см) и в миллиметрах (мм) или же площадь её основания и высоту, которые перемножаются. Результат математического действия переводится в нужную единицу измерения (м3, см3, мм3). Сделать это можно и до выполнения расчёта.

расчет количества кубе досок 40х150х6000

Во многих случаях измерение количества того или иного материала удобнее осуществлять не определением его массы (веса), а объёма, что позволяет не обращать внимания на плотность, зависящую от влажности, например. Если массы влажной и сухой доски отличаются значительно, то разницей их объёмов можно пренебречь и считать равными.

Доска строганая относится к одним из самых популярных строительных материалов. Толщина её может быть различной и выбирается, исходя из предназначения материала. Чтобы узнать, сколько строганых досок в одном кубометре необходимо определить объем одной из них, для чего перемножаются значения её длины, ширины и толщины, измеренные в метрах. В нашем примере это выглядит так: 6*0,15*0,04 = 0,036 м³. После этого не составит особой сложности определение количества досок, «спрятанных» в одном кубометре:

1: 0,036 = 27,777 шт.

Объем 27 досок будет меньше кубометра, а 28 — больше. Это следует учитывать при заказе больших объёмов, которые приведут к значительным погрешностям. Так, если требуется 280 штук досок, то заказывая 10 кубометров, можно получить 278 штук, которых недостаточно. Поэтому при заказе необходимо исходить из 27 досок в кубе. Тогда нужно будет докупить ещё пару досок, о нехватке которых будет известно перед отправлением в магазин.

На фото показана таблица расчета

Разницей количества досок в кубометре умело пользуются недобросовестные продавцы, округляя в выгодную для себя сторону. Так, продавая 27 досок, они берут денег с покупателя за один кубометр. Если таких покупателей будет много, то «выручка» продавцов составит значительную сумму.

Как рассчитывается доска на практике?

Расчёт необходимого количества досок осуществляется, исходя из площади, которую нужно ими покрыть. Пусть это будет, например, пол помещения, размеры которого составляют 50 на 10 метров. Площадь пола в этом случае составит 500 м². Площадь одной доски в нашем примере составляет 0,9 м² (6*0,15). Деление 500 на 0,9 позволит определить, что досок нужно 555,555 штуки. Так как отпускается доска в кубометрах, количество нужно перевести в кубометры, умножив последний результат (555,555) на объём 1-й доски (0,036). В результате получится почти 20 м³. Заказ в 20 м³ позволит получить требуемое количество досок с некоторым запасом.

Чтобы не заниматься расчётами, создана специальная таблица кубатурника обрезной доски. Она имеется у всех компаний, специализирующихся на сбыте материалов из древесины.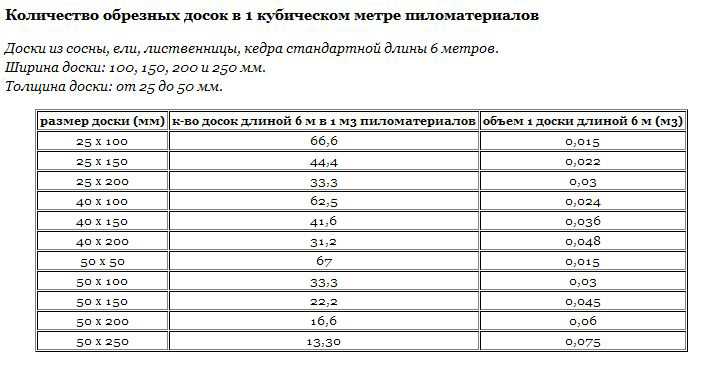 В них включены все ходовые пиломатериалы с указанием размеров, что позволяет быстро и точно определить объем нужного материала, количество в штуках, а также покрываемую ими площадь.

Кубатурник досок таблица:

Размер, мм	Кол-во штук в одном м³	Кол-во погонных метров в одном м³	Объём одной доски, м³	Площадь одной доски, кв.м.	Вес одной доски, кг (влажн. 20%)
20х100х6000	83,3	500	0,012	0,6	9
20х100х3000	167,6	500	0,006	0,3	4,5
20х150х6000	55,6	333,3	0,018	0,9	13,5
20х150х3000	111,1	333,3	0,009	0,45	6,75
22х100х6000	75,8	454,5	0,0132	0,6	9,9
22х100х3000	151,5	454,5	0,0066	0,3	4,95
22х125х6000	60,6	363,6	0,0165	0,75	12,375
22х125х3000	121,2	363,6	0,00825	0,0375	6,19
22х150х6000	50,5	303	0,0198	0,09	14,85
22х150х3000	101	303	0,0099	0,045	7,425
22х175х6000	43,3	259,7	0,0231	1,05	17,325
22х175х3000	86,6	259,7	0,01155	0,525	8,66
22х200х6000	37,9	227,3	0,0264	1,2	19,8
22х200х3000	75,8	227,3	0,0132	0,6	9,9
22х225х6000	33,7	202	0,0297	1,35	22,275
22х225х3000	37,3	202	0,01485	0,675	11,138
22х250х6000	30,3	181,8	0,033	1,5	24,75
22х250х3000	60,6	181,8	0,0165	0,75	12,375
25х100х6000	66,7	400	0,015	0,6	11,25
25х100х3000	133,3	400	0,0075	0,3	5,625
25х100х2000	200	400	0,005	0,2	3,75
25х125х6000	53,3	320	0,01875	0,75	14,06
25х125х3000	106,7	320	0,009375	0,0375	7,03
25х150х6000	44,4	266,7	0,0225	0,9	16,875
25х150х3000	88,9	266,7	0,01125	0,45	8,44
25х150х2000	133,3	266,7	0,0075	0,3	5,625
25х175х6000	38,1	228,6	0,02625	1,05	19,69
25х175х3000	76,2	228,6	0,012125	0,525	9,094
25х200х6000	33,3	200	0,03	1,2	22,5
25х200х3000	66,7	200	0,015	0,6	11,25
25х225х6000	29,6	177,8	0,03375	1,35	25,31
25х225х3000	59,3	177,8	0,016875	0,675	12,656
25х250х6000	26,7	160	0,0375	1,5	28,125
25х250х3000	53,3	160	0,01875	0,75	14,06
32х100х6000	52,1	312,5	0,0192	0,6	14,4
32х100х3000	104,2	312,5	0,0096	0,3	7,2
32х125х6000	41,7	250	0,024	0,75	18
32х125х3000	83,3	250	0,012	0,0375	9
32х150х6000	34,7	208,3	0,0288	0,9	21,6
32х150х3000	69,4	208,3	0,0144	0,45	10,8
32х175х6000	29,8	178,6	0,0336	1,05	25,2
32х175х3000	59,5	178,6	0,0168	0,525	12,6
32х200х6000	26	156,3	0,0384	1,2	28,8
32х200х3000	52,1	156,3	0,0192	0,6	14,4
32х225х6000	23,1	138,9	0,0432	1,35	32,4
32х225х3000	46,3	138,9	0,0216	0,675	16,2
32х250х6000	20,8	125	0,048	1,5	36
32х250х3000	41,7	125	0,024	0,75	18
40х100х6000	41,7	250	0,024	0,6	18
40х100х3000	83,3	250	0,012	0,3	9
40х125х6000	33,3	200	0,03	0,75	22,5
40х125х3000	66,7	200	0,015	0,0375	11,25
40х150х6000	27,8	166,7	0,036	0,9	27
40х150х3000	55,6	166,7	0,018	0,45	13,5
40х175х6000	23,8	142,9	0,042	1,05	31,5
40х175х3000	47,6	142,9	0,021	0,525	15,75
40х200х6000	20,8	125	0,048	1,2	36
40х200х3000	41,7	125	0,024	0,6	18
40х225х6000	18,5	111,1	0,054	1,35	40,5
40х225х3000	37	111,1	0,027	0,675	20,25
40х250х6000	16,7	100	0,06	1,5	45
40х250х3000	33,3	100	0,03	0,75	22,5
50х100х6000	33,3	200	0,03	0,6	22,5
50х100х3000	66,7	200	0,015	0,3	11,25
50х125х6000	26,7	160	0,0375	0,75	28,125
50х125х3000	53,3	160	0,01875	0,0375	14,06
50х150х6000	22,2	133,3	0,045	0,9	33,75
50х150х3000	44,4	133,3	0,0225	0,45	16,875
50х175х6000	19	114,3	0,0525	1,05	39,375
50х175х3000	38,1	114,3	0,02625	0,525	19,688
50х200х6000	16,7	100	0,06	1,2	45
50х200х3000	33,3	100	0,03	0,6	22,5
50х225х6000	14,8	88,9	0,0675	1,35	50,625
50х225х3000	29,6	88,9	0,03375	0,675	25,31
50х250х6000	13,3	80	0,075	1,5	56,25
50х250х3000	26,7	80	0,0375	0,75	28,125
60х125х6000	22,2	133,3	0,045	0,75	33,75
60х125х3000	44,4	133,3	0,0225	0,0375	28,125
60х150х6000	18,5	111,1	0,054	0,9	40,5
60х150х3000	37	111,1	0,027	0,45	20,25
60х175х6000	15,9	95,2	0,063	1,05	47,25
60х200х6000	13,9	83,3	0,072	1,2	54
60х225х6000	12,3	74,1	0,081	1,35	60,75
60х250х6000	11,1	66,7	0,09	1,5	67,5
60х250х3000	22,2	66,7	0,045	0,75	33,75
75х175х6000	12,7	76,2	0,07875	1,05	59,06
75х175х3000	25,4	76,2	0,0394	0,525	29,55
75х200х6000	11,1	66,7	0,09	1,2	67,5
75х200х3000	22,2	66,7	0,045	0,6	33,75
75х225х6000	9,9	59,3	0,101	1,35	75,75
75х225х3000	19,7	59,3	0,051	0,675	38,25
75х250х6000	8,9	53,3	0,1123	1,5	84,225

Приобретая древесные строй материалы, необходимо учитывать их влажность и неизбежные отходы, чтобы завезённых материалов хватило без большого остатка. Поэтому к определению потребного количества таких строительных материалов нужно подходить ответственно, чтобы не понести лишние расходы.

Кубик Рубика

Что такое кубик Рубика? топ

……	Кубик Рубика — это головоломка в форме куба. На первый взгляд состоит из 27 маленьких кубиков, которые составляют вместе куб 3x3x3.

……	На самом деле их 21 штука: 1 основная часть с тремя оси, 8 уголков (угловых кубиков) трех цветов и 12 краев (реберные кубики) двух цветов.

Цвета моего куба: белый/желтый, оранжевый/красный (здесь: оранжевый = розовый) и зеленый/синий. После нескольких случайных ходов кубик окрашивается.

Если куб собран, все боковые грани одного цвета.
Главная задача — собрать куб ;-).

Решение журнала SPIEGEL слегка измененный
Вводный вверху
Эрнё Рубик, венгерский профессор физики и дизайна, изобрел кубик в 1974 году. Около 1980 года кубик Рубика распространился по всему миру. по всему миру, как вирус. В начале 80-х около 100 млн кубов были проданы по всему миру. Люди пытались ее решить. Но большинство из них придерживались один ломтик или два ломтика.
В Германии журнал DER SPIEGEL опубликовал первую решение, которое вы могли бы понять. Это решение до сих пор актуально интерес.
Авторские права принадлежат газете SPIEGEL и журналисту Альбрехту. Кункель.

На следующих семи картинках показано, как собирается куб.
(Изображение 4 и Изображение 6 могут отличаться.)

Повороты ломтиков показаны квадратом 3×3 и Стрелка.

Квадраты всегда являются передними квадратами, стрелка описывает на четверть оборота в направлении стрелки. Стрелки находятся в срезе ты должен повернуться.
На рисунке напротив показано значение квадратов со стрелками в двух примерах.

Это более практично. .

Помните один принцип в следующем семь шагов этого решения:
Никогда не поворачивайте сам куб, но только отдельные ломтики во время поворота. Это означает ориентацию куба в пространстве всегда одинакова при вращении.

Строительство Первый Срез топ
Решая первый и средний срез, вы должны удерживать куб так, чтобы белый центр грани был вверху.

1-й шаг: Решение реберных кубов.
Вы ищете синий/белый реберный куб и поворачиваете его в спереди/снизу/посередине.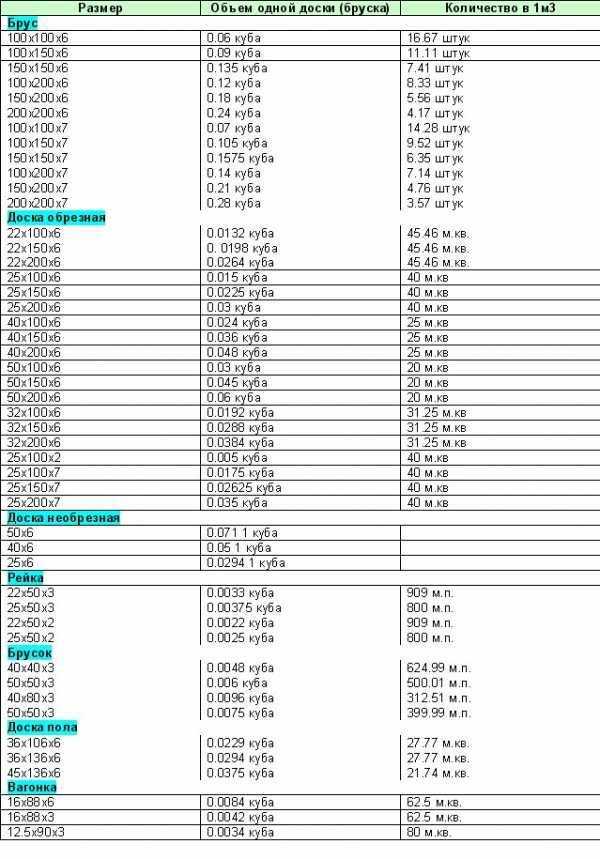
Есть две возможности 1a) или 1b).
1a) белый снизу

1b) белый спереди

Вы повторяете ходы с оранжевым, зеленым и красным лица точно так же.
Результат: Сверху белый крест. Цвета реберных кубов и центр четырех граней имеют одинаковый цвет. (Изображение 1 из 7)

2-й шаг: Решение угловых кубов.
Есть четыре угловых кубика белого цвета. Ты держите куб так, чтобы белый был вверху, а синий впереди.
Напр. вам нужно переместить угловой куб белый/красный/синий в правильное положение спереди/справа/сверху.
Сначала переместите этот куб на место спереди/вниз/влево.
Есть три возможности 2a), 2b) или 2c).
2а) белый левый

2b) белый спереди

2c) белый снизу

Таким же образом вы поступите с тремя оставшимися белыми углами.

кубики.
Результат: Верхний срез полностью белый. Цвета краевых кубов соответствуют центральным кубам.

Строительство Средний срез сверху
3-й шаг
В среднем срезе перемещайте только четыре краевых кубика синего/оранжевого цвета, синий/красный, зеленый/оранжевый и зеленый/красный. Вы должны сделать это, начав с нижний. Вы держите куб так, чтобы белый был наверху.
Вы должны повернуть нижний срез так, чтобы один из краев кубики синего/оранжевого или синего/красного цвета спереди/снизу/посередине. Есть две возможности 3а) или 3б).
3а) направо

3б) налево

Если внизу отображается синий квадрат, вы начинаете с другого цвет.
Если все кубы находятся в средней части, переместите куб вниз в середину одной из последовательностей 3а) или 3б).

Результат: Верхний и средний фрагменты находятся в правильные позиции.

Строительство последний слайс топ
Вы поворачиваете куб, чтобы собрать последний фрагмент (белый снизу, желтый вверху).

4-й шаг: Поменяйте местами два кубика.
Вы поворачиваете один из четырех крайних кубов желтым/синим, желтым/оранжевым, желтый/зеленый, желтый/красный к лицу с правильным цветом (если желтый не наверху, не волнуйтесь!). Если остальные кубики не в правильных позициях, вы должны переключить их через левый край куба наверху. Вероятно, вам придется повторить эту последовательность. (Картина 4 из 7)

5-й шаг: Переверните реберные кубики
Хотя все реберные кубы находятся в правильном положении, они могут ошибаться. Желтый не на высоте.
Вы должны перевернуть их. Вы держите куб так, чтобы реберный куб справа/сверху/посередине. Теперь восемь ходов.

Если куб стал цветным после этих 8 ходов, идите дальше. Поверните следующий реберный куб, чтобы перевернуть его в то же место вправо/вверх, повернув весь кусочек (не переворачивайте весь кубик). Затем восемь ходов опять таки.
Результат: Желтый крест. Вы поворачиваете верхний ломтик так, чтобы краевые кубы были в правильных местах.

6-й шаг: Поменять местами три угла кубики
Сначала вы перемещаете четыре оставшихся угловых кубика на правильные позиции. Их цвета не обязательно должны быть правильными.
Если все четыре угловых кубика находятся в правильном положении, то следующая последовательность не нужна.
Если все четыре угловых кубика находятся не в том месте после выравнивая , то есть еще 22 хода:

Если все четыре угловых кубика по-прежнему не на своих местах, Вы должны повторить восемь ходов.

Лицевая сторона должна оставаться впереди.
После этих ходов один угловой кубик находится на нужном месте. Поверните куб так, чтобы этот угловой куб был сзади/слева. Теперь вы повторяете восемь ходов. Результат: Четыре угловых кубика на своих местах.

Комментарии к 6 шагу
Вскоре после публикации (4/1981) появилось решение задачи «переключение положения трех угловых кубиков», которые я сейчас описываю. Вам нужно всего 8 ходов вместо 22.

Ич скажу эту аббревиатуру условно.

7-й шаг: Вращение угловых кубиков.
Цвета углового куба должны измениться.
Вы держите куб так, чтобы угловой куб оказался сверху/справа/спереди. Затем восемь ходов.

Если желтый цвет не находится на вершине этого специального углового куба, вы повторяете эти восемь ходов.
Затем вы переворачиваете верхний срез (не весь куб), так что что следующий угловой куб находится сверху/справа/спереди.

Вы повторяете ходы 8 или 2×8.
Если все четыре угловых кубика повернуты, желтый должен быть на высоте. Теперь последний шаг. Переверните последний кусочек. Шесть лиц иметь один цвет. ЗАКОНЧЕННЫЙ!

Планируется Хаос топ
Можно ли повернуть куб так что у вас есть каждый цвет на каждом лице хотя бы один раз? Да, это так.
(Начните с синего цвета спереди, белый вверху)

Взятие на Кусочки верх
Вы также можете собрать куб, разобрать и собрать.
Есть некоторые продукты с винт в центре грани. Вы можете открутить его. Тогда вы сможете решить куб.
Большинство товаров можно разобрать только с небольшим усилием.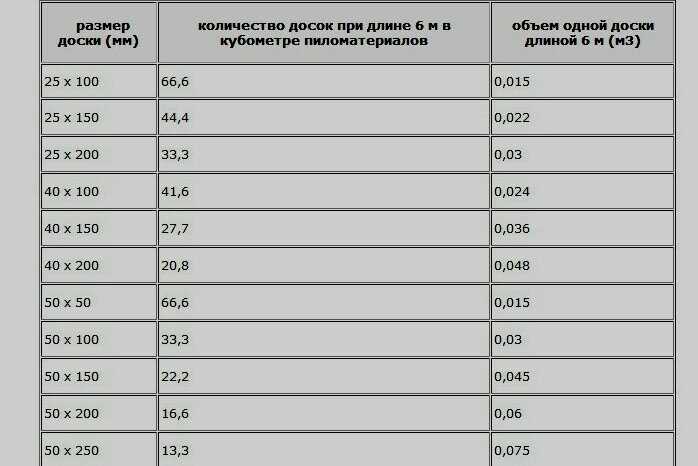 Вы поворачиваете верхний срез примерно на угол 45 градусов. Приподнимаете верхний срез отверткой или ручкой ложки осторожно . В этом положении вы можете удалить реберный куб, а затем соседний угол кубики.

Если вы очень умны, вы собираете кубик, удаляя клейкие пленки и приклеивание их снова ;-).

Решение с секундомером сверху
Те, кто сможет собрать кубик, увидят следующая задача: собрать куб как можно быстрее.
Время решения куба равно другой. Это зависит от расположения кубиков в начале. Но есть средние сроки.
Требуются профессиональные токарные станки не более 90 ходов. Они знают множество последовательностей, позволяющих реагировать на них. к особым ситуациям соответствующим образом. Они не решают куб шаг за шагом шаг. Вместе они видят множество кубиков.
Кроме того, они используют силиконовое масло.

В «Guiness Buch der Rekorde» 1986″ вы найдете:
5 июня 1982 г. Мин Тай, США выиграл чемпионат по сборке кубика Рубика в Будапеште. Его время: 22.95 с.

Решение куб с маленькими числами последовательностей вверху
Большинство людей предпочитают метод с небольшим количеством последовательностей (не ходов). Если вы соберете куб, вы не хотите смотреть на бумагу, вы решаете ее наизусть.
В этом отношении решение SPIEGEL хороший.
Если у вас есть практика, вы можете заказать первый кусок легко. Шаг 2с) не нужен, можно использовать 2а) и 2б). Вам нужны только последовательности не более восьми ходов.
Тем не менее вам нужно от 120 до 180 ходы, потому что вам придется повторять последовательности снова и снова. Если у вас есть не повезло вам нужно 75 ходов для последнего шага «Вращение углового куба». Куб можно решить методом Шпигеля за 2-3 минуты.

Некоторые Математика топ
В книге Трайбера (3) есть является математической теорией куба.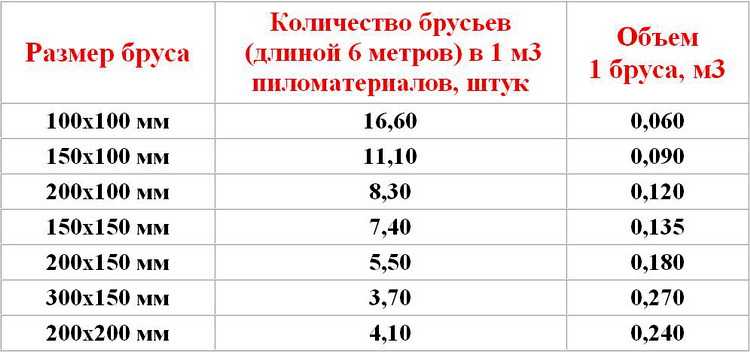
Вы нумеруете квадраты, которые вы можете перемещать, от 1 до 48 (48 = 6х9-6). Ход или последовательность ходов приводит вас к новой аранжировке из чисел от 1 до 48. Это называется «перестановкой». Все перестановки сформировать «группу».
Так что вместо того, чтобы смотреть в кубик Рубика, вы можете занять себя с группой.
Перенесен один интересный момент в теории групп к кубу:
Если вы повторяете ход или последовательность ходов, вы всегда вернуться к началу.

Если вы хотите потренироваться с последовательностями решения SPIEGEL вы делаете это следующим образом: 920 комбинаций из 54 квадратов, если разобрать кубик и собрать его вместе.
Появляется 43 252 003 274 489 856 000 комбинаций (1/12) на кубе во время поворота.

Выкройки верх
Широкое поле деятельности — поиск новых закономерностей.
Вот пример, который вы можете развить, чтобы найти больше узоры. (Каждая стрелка означает четверть оборота. )

Если вы повторите последовательность, вы вернетесь к решенному кубу.

Варианты:

……	Если вы начинаете не с собранного куба, а с одного вариант слева, вы получаете новые узоры.

Если перевернуть ломтики другим способом, то получатся новые узоры, слишком.

Вы получаете 12 шаблонов:

Рубика Куб в Интернете топ

немецкий

Ларс Петрус
Рубика Zauberwürfel auf Zeit lösen

Оливер Райманн
Анлейтунг für den Zauberwürfel

Рекорд-Клуб Саксония
Рубика куб

Рональд Бибер
Рубика куб

Сигрун Дьюэсс
Рубик-Цаубервюрфель порядок

Шпигель-Виссен
Шрей Ура! Шмайсс ‘не Рунде!
Die Spiegelausgabe 4/1981 vom 19. 01.1981 ist jetzt (февраль 2008) для частной компании Gebrauch freigegeben! 🙂

Урс Мансер
Рубика Куб (Лёсунг)

Википедия
Заубервюрфель

Английский

Жорж ХЕЛМ
Коллекция кубики Рубика и связанные с ними головоломки

Яап Шерфуис
Рубика Куб 3x3x3, бочонок/восьмиугольник

Джессика Фридрих
Мой страница скоростного куба

Ларс Петрус
Сбор кубика Рубика для скорости

Надер (naderc)
резюме Рубик — Компьютер видит кубик Рубика и собирает его (Решение Шпигеля как видео)

Рубик онлайн
Официальная домашняя страница Эрнё Рубика

Стефан Похманн
Стефан Кубический уголок Похманна

Википедия
Рубика куб

Каталожные номера (немецкий) вверх
(1) DER SPIEGEL Nr.4/1981
(2) Йозеф Трайбер: Der Würfel, Niedernhausen/Ts.

1981 (Фалькенферлаг 0565)
(3) Йозеф Трайбер: Der Würfel für Fortgeschrittene, Нидернхаузен/Ц. 1981 (Фалькенферлаг 0590)
(4) Том Вернек: Der Zauberwürfel, Мюнхен 1982 (Хейн 4831)
(5) Том Вернек: Der Zauberwürfel für Könner, Мюнхен 1982 (Хейн 4834)
(6) Курт Эндл: Rätsel des Jahrhunderts Рубика, Гиссен 1981
(7) Александр Х.Фрей-младший и Дэвид Сингмастер: Справочник Cubik Math, Хиллсайд, Нью-Джерси, 1982 [ISBN 0-89490-060-9]

Обратная связь: Адрес электронной почты на моей главной странице

Это страница также доступна на немецком языке.

URL-адрес моя домашняя страница:
http://www.mathematische-bastelien.de/

наверх

Обзор кубика Рубика и размышления о его применении в механизме | Китайский журнал машиностроения

Обзор
Открытый доступ
Опубликовано: 27 августа 2018 г.

DA-XING Zeng ¹,
Ming Li ¹,
JUAN-JUAN WANG ¹,
YU LEI LEI ¹,
YU LEI LOI LEI ¹,
yuan ¹,
yuan ¹,
yuan ¹,
yuan ¹,
.
…
Чжэнь Хуан ¹

Китайский журнал машиностроения том 31 , Номер статьи: 77 (2018) Процитировать эту статью

114 тыс. обращений
8 Цитаты
6 Альтметрический
Сведения о показателях

Abstract

Кубик Рубика — широко популярная механическая головоломка, которая привлекла внимание во всем мире благодаря своим уникальным характеристикам. Как классическая игрушка для тренировки мозга, хорошо известная публике, кубик Рубика использовался многими учеными для научных исследований и разработки технологий. Эта статья дает базовое понимание кубика Рубика и показывает его механическое искусство с точки зрения происхождения и развития, характеристик, исследовательского статуса и особенно его машиностроительного дизайна, а также дает представление о применении в механизме. Сначала представлены изобретение и происхождение кубика Рубика, а затем анализируются особенности самого кубика. После этого нынешние исследования кубика Рубика рассматриваются в различных дисциплинах в стране и за рубежом, включая исследования научных метафор кубика Рубика, алгоритмов сокращения, характерных приложений и вопросов механизма. Наконец, обсуждаются приложения и перспективы кубика Рубика в области механизмов.

Введение

Кубик Рубика — это трехмерная комбинированная головоломка, изобретенная в 1974 году венгерским скульптором и профессором архитектуры Эрно Рубиком [1] и первоначально называвшаяся Волшебным кубиком [2, 3]. Это изобретение вызвало широкий интерес в мире благодаря своим уникальным характеристикам, оказавшим глубокое влияние на человечество. Кубик Рубика входит в число 100 самых влиятельных изобретений 20-го века [4]. Кроме того, она считается самой продаваемой игрушкой в мире [5]. Он получил специальную награду «Игра года в Германии» [6] и получил аналогичные награды за лучшую игрушку в Великобритании, Франции и США. [7].

Хотя кубик Рубика достиг пика своей популярности в 1980-х годах, он по-прежнему широко известен и используется. Он не только привлекает энтузиастов кубика Рубика, проводящих исследования алгоритмов сокращения кубика Рубика [8,9,10], но также привлекает внимание ученых и технических работников из различных слоев общества своим сложным дизайном и идеями [11]. С одной стороны, структура кубика Рубика имеет несколько особенностей, таких как вращение, перестановки и комбинации, а также цикл и симметрия, которые рассматривались как физические модели или инструменты для изучения конкретных научных вопросов или изучались с использованием научной теории или методов в некоторых областях. {2} + 1)/2\). Это называется константой магического квадрата. Постоянная магического квадрата куба третьего порядка равна 15 [13].

Переставить Цзюгун — это одномерный куб третьего порядка, игра, разработанная на основе карты Цзюгун примерно во времена китайской династии Юань. В этой игре восемь подвижных фигур размещаются в девяти местах на доске, перемещая фигуры, чтобы создать еще один шаблон, чтобы завершить изменение шаблона «Переставить цзюгун».

Перегруппировка Jiugong распространилась на запад, и Сэм Лойд изобрел на ее основе 15 шахмат. Принцип 15 шахмат (перемещение фигур для изменения рисунка) такой же, как и в перестановке цзюгун. Однако шахматы порядка 15 представляют собой куб четвертого порядка, который на один порядок выше, чем Переставить Цзюгун.

После этого развитие куба перешло от порядка к измерению. Во времена династии Цин китайские ученые выдвинули идею использования цифровых фрагментов трехмерных магических квадратов. На самом деле это был прототип трехмерного куба второго порядка, как показано на рисунке 2.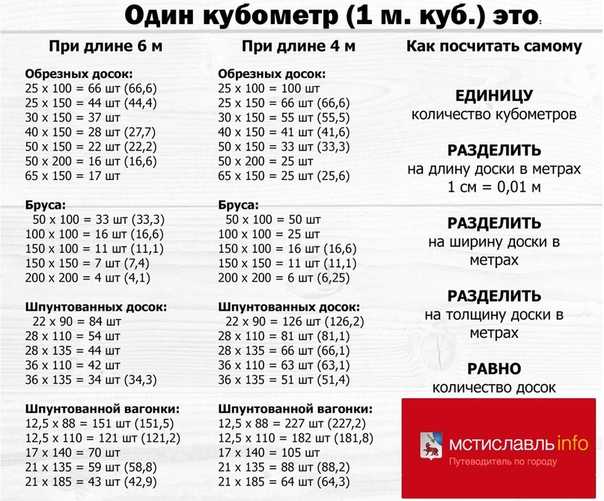

Рисунок 2

Трехмерный магический квадрат

Изображение в полный размер до тех пор, пока Рубик не спроектировал вращающийся механический куб в 1974. Японский каменный мех в одиночку завершил тот же дизайн в 1976 году. Принцип перемещения частей для достижения изменения рисунка аналогичен перестановке цзюгонга за счет перемещения частей для достижения общих изменений. Основной принцип заключается в том, что путь движения фигуры ограничивается другими частями, которые соприкасаются с ней.

Рубик сделал первый в мире куб третьего порядка, который выглядит как сфера и управляется ограничениями между компонентами для достижения определенного вращения. Это показано на рис. 3. Изначально, с учетом соображений безопасности, восемь вершин куба были немного обрезаны. Позже он был изменен на острые углы и стал кубической формы, потому что его вершина не влияла на внешний вид, а процесс производства упростился. Современный обычный куб третьего порядка показан на рисунке 4. Видно, что форму кубика Рубика можно изменить, не влияя на вращение структуры куба.

Рисунок 3

Ранний кубик Рубика

Полноразмерное изображение

Рисунок 4

Текущий кубик Рубика

Полноразмерное изображение

Для расширения семейства кубиков Рубика1 было изобретено множество модифицированных кубиков [4 ]. Как правило, магический куб можно разделить на две категории: кубический куб и куб специальной формы. Кубический куб относится к кубу в блочной структуре, которая не изменяется, но порядок куба увеличивается. Существуют различные варианты кубиков Рубика с количеством слоев до 33: с 2 × 2 × 2 (карманный/мини-кубик), стандартным кубиком 3 × 3 × 3, 4 × 4 × 4 (Месть Рубика/мастер-кубик) и 5 × 5 × 5 (Профессорский куб) самый известный. Куб 17 × 17 × 17 «Over the Top» (доступен в конце 2011 г.) до декабря 2017 г. был самым большим (и самым дорогим, стоимостью более 2000 долларов США) коммерчески продаваемым кубом. Рабочий проект для куба 22 × 22 × 22 существует и был продемонстрирован в январе 2016 года [15], а куб 33 × 33 × 33 был представлен в декабре 2017 года [16]. Китайский производитель ShengShou выпускал кубы всех размеров от 2 × 2 × 2 до 10 × 10 × 10 (по состоянию на конец 2013 г.) [17], а также выпускал модель 11 × 11 × 11. На рис. 5 перечислены шесть вариантов куба.

Рисунок 5

Модели кубика Рубика

Изображение в полный размер

Куб особой формы относится к семейству кубиков, помимо кубического куба. Структурная форма куба специальной формы разнообразна, включая кубы многогранника, куба сферы, куба тетраэдра, зеркального куба, куба шестеренки, куба торта и так далее. На рис. 6 перечислены шесть случаев кубов особой формы.

Рисунок 6

Кубики особой формы

Изображение в полный размер

Уже 19 лет59 был изобретен куб второго порядка, вращение которого зависит от магнетизма. Однако этот кубик менее популярен, чем кубик Рубика, вращение которого в последнем основано на механическом вращении. С одной стороны, стоимость куба слишком высока из-за его магнитной структуры и преобладающих факторов рыночной экономики. С другой стороны, куб второго порядка трудно восстановить. Затем Рубик изобрел кубик третьего порядка, который имеет компактную структуру, продуманный дизайн и низкую стоимость, тем самым преодолев врожденные недостатки магнитного кубика второго порядка. Короче говоря, особая механическая структура внутри является ключом к изобретательности кубика Рубика.

Характеристики кубика Рубика

Структурная характеристика вращения

Структура механизма кубика Рубика — самый замечательный аспект кубика. Поначалу кажется, что Cube вообще не может работать. Очень немногие предложили возможный механизм, и очень немногие из них оказались практичными. Позже многие механизмы кубика Рубика были основаны на врезных и шиповых соединениях между деталями, как показано на рисунке 7.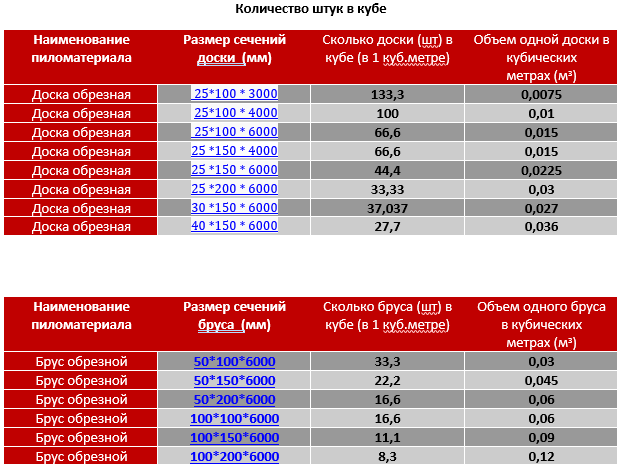

Рисунок 7

Три вида врезных и шиповых соединений кубика Рубика

Изображение в полный размер

Механизм Рубика имеет соединения, как показано на рисунке 7 (c), что значительно упрощает форму деталей. Можно использовать методы врезки и шипа, чтобы 26 внешних частей куба скреплялись вместе без центральной части. Это соединение трудно выполнить с достаточной точностью, чтобы грани легко поворачивались [18].

На рисунке 8 стандартный куб 3 × 3 × 3 состоит из 26 уникальных миниатюрных кубов, также называемых «элементами» или «кублетами», включая центральную раму, 6 центральных элементов, 8 угловых элементов и 12 краевых элементов. Различные типы деталей кубика Рубика показаны на рисунке 9.. Каждая из них включает в себя скрытое внутреннее расширение, которое сцепляется с другими частями, позволяя им перемещаться в разные места.

Рисунок 8

Кубик Рубика

Полноразмерное изображение

Рисунок 9

Структура блока кубика Рубика

Полноразмерное изображение

На рисунке 10 показано, что центральную часть можно разделить на две части. Центральная часть и рама центрального вала соединены подпружиненными винтами, как показано на рис. 11.

Рисунок 10

Центральная деталь в разобранном виде

Изображение в полный размер

Рисунок 11

Подпружиненные винты

Изображение в полный размер

На рисунке 12 показан процесс сборки различных частей по одной. Ограничения на ребрах формируются структурными ограничениями и силовым замыканием двух соседних центров. Ограничения на угловой элемент формируются конструктивными ограничениями и силовым запиранием трех соседних краев.

Рисунок 12

Процесс сборки четырех типов деталей

Изображение в полный размер

Способы контакта между центрами и краями, а также краями и углами показаны на рисунке 13. Все они контактируют друг с другом плоскостью и криволинейная поверхность.

Рисунок 13

Режим контакта между различными деталями

Изображение в полном размере

Ножки (удлинение внутрь) угловых и краевых частей плотно соединены крючком.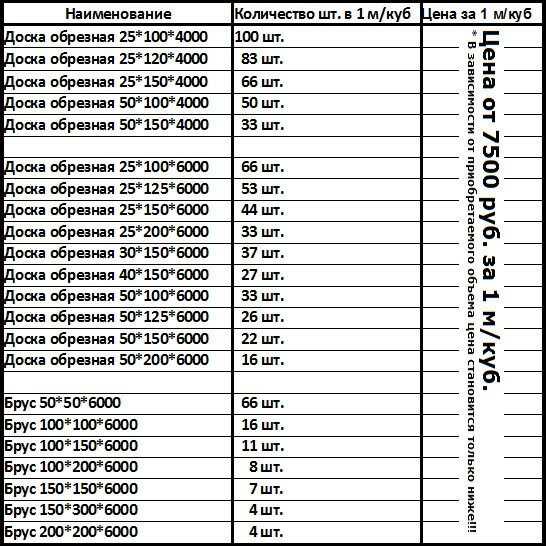 Они образуют патрон, похожий на зажимную часть машины, как показано на рисунке 14(а). С одной стороны, девять маленьких кусочков, как показано на рисунке 14(b), плотно сжаты, чтобы они не могли расползаться. С другой стороны, слой кубика Рубика может гибко вращаться вокруг вала при приложении силы.

Рисунок 14

Внутренняя структура кубика Рубика

Изображение в полный размер

Характеристика кубика Рубика, в котором маленькие кусочки соединяются друг с другом взаимной мозаикой, аналогична Любанскому замку, который был изобретен на основе принципа метафизики сплетен. . Замок Любань — традиционная китайская интеллектуальная игрушка. Он возник из скелетных структур древней китайской архитектуры. Его части скреплены структурными ограничениями без каких-либо гвоздей или веревок. Взаимоотношения между различными частями сложны.

На рис. 15 представлен шариковый замок Luban, который собирается из шести деревянных элементов, которые можно соединить вместе. Шесть деревянных деталей показаны на рисунке 16. При сборке деревянные детали скрепляются вместе, оставляя место для вставки задних компонентов до тех пор, пока не будет размещена последняя часть «замочной скважины». Весь Любанский замок прочно скреплен, части сдерживают друг друга и поддерживают друг друга. Комбинированная структура кубика Рубика происходит от конструкции приседаний замка Любана.

Рисунок 15

Замок Ball Luban после сборки

Полноразмерное изображение

Рисунок 16

Части замка Ball Luban

Изображение в полный размер

Шесть вариантов конструкции замка Luban показаны на рисунке 17 и шиповые конструкции. соединяются соединительным методом вогнуто-выпуклой обработки. Это свидетельствует о большом творчестве и достижениях древних.

Рисунок 17

Любанский замок

Увеличенное изображение

На устойчивость врезной и шиповой конструкции влияют такие факторы, как расположение канавок, плотность лоскутного шитья и степень герметичности траншеи. Успех соединения врезной и шиповой конструкции зависит от того, насколько точно будут соединены детали разного размера. Весь замок развалится, когда деревянную планку уберут. И в замке Любана, и в кубике Рубика используются мозаичные структуры для достижения общей устойчивости. Отличие кубика Рубика от замка Любана в том, что кубик Рубика может перевернуть слой, приложив к нему силу, а замок Любана не может.

Перестановка и комбинация Характеристика

Комбинаторика возникла из книги восточных луо, и идея перестановки и комбинации была предложена для удовлетворения потребностей человека в счете [13]. Древние китайские восемь диаграмм, календарь Небесных стеблей и Земных ветвей, а также некоторые методы гадания содержат концепции перестановки и комбинации. Восемь диаграмм могут описывать пространственную систему координат кубика Рубика и соответствовать декартовой системе координат один в один. Они показывают, что преобразование вращения кубика Рубика содержит идеи перестановки и комбинации. Кубик Рубика достигает желаемого состояния и всевозможных комбинаций цветов, вращая части.

Оригинальный (3 × 3 × 3) кубик Рубика имеет шесть граней. Изначально каждая грань имеет один и тот же цвет, и каждая грань имеет девять маленьких внешних поверхностей. Всего у них 54 внешних поверхности. Каждая сторона кубика Рубика состоит из кусочков разного цвета после случайного вращения разных сторон несколько раз.

Оригинальный (3 × 3 × 3) кубик Рубика имеет 8 углов и 12 ребер. Углов можно расставить по 8! (40 320) способов, и существует 3 ⁷ (2187) возможных ориентаций, поскольку ориентация восьмого (последнего) угла зависит от предыдущих. Края можно расположить 12!/2 (239{11} = 4 3 2 5 2 0 0 3 2 7 4 4 8 9 8 5 6 0 0 0 $ $

, что составляет примерно 43 квинтиллиона [19].

Преобразование различных конфигураций кубика Рубика можно использовать как режим, использующий идею перестановок и комбинаций для достижения разнообразия ответов. Характеристики комбинирования и преобразования вдохновляют на размышления о дизайне продукта и имеют практическую ценность, особенно в модуляризации промышленных продуктов и структурном проектировании [20].

Характеристика цикла

Циркуляция — одна из основных характеристик кубика Рубика. Если использовать произвольную последовательность операций (последовательность вращения) для циклической работы куба, он получит статус цикла. Циклическую характеристику работы можно разделить на две категории: периодическую и непериодическую [12].

Если предположить, что кубик Рубика управляется определенными числовыми операциями и заданными операциями из исходного состояния обратно в исходное состояние снова, это означает, что кубик Рубика выполняет цикл. Период обращения — это количество оборотов кубика Рубика. Если период обращения постоянен, цикл является периодическим. Если период обращения переменный, цикл непериодический. Последовательность операций непериодического цикла основана как на последовательности периодических циклических операций, так и на последовательности операций «постоянного процесса», которая вызывает непериодические изменения структуры куба. Последовательность операций «постоянного процесса» относится к тому факту, что все части могут вернуться в исходное состояние после этой последовательности операций.

Исследовательский статус кубика Рубика

После успешного изобретения первого кубика Рубика в Венгрии была изготовлена группа коммерческих кубиков. Кубик Рубика был признан лучшей игрушкой на международной ярмарке в Нюрнберге, Германия, в 1978 году, а его изобретатель Рубик был удостоен награды «Лучшее игровое изобретение мира». С тех пор популярность кубика Рубика распространилась по всему миру. В то же время в Хельсинки проходила международная представительная конференция математиков. Кубик Рубика привлек большое внимание специалистов и исследователей. После этого постоянно публиковались статьи и заметки о кубике Рубика, и дверь для изучения тайн кубика Рубика была открыта.

Научная метафора кубика Рубика

Научная метафора кубика Рубика имеет два значения. Во-первых, проблема куба изучается с использованием существующей научной теории или методов. Дэвид [21, 22] выдвинул набор стандартных символов кубика Рубика с учетом комбинаторики и теории групп.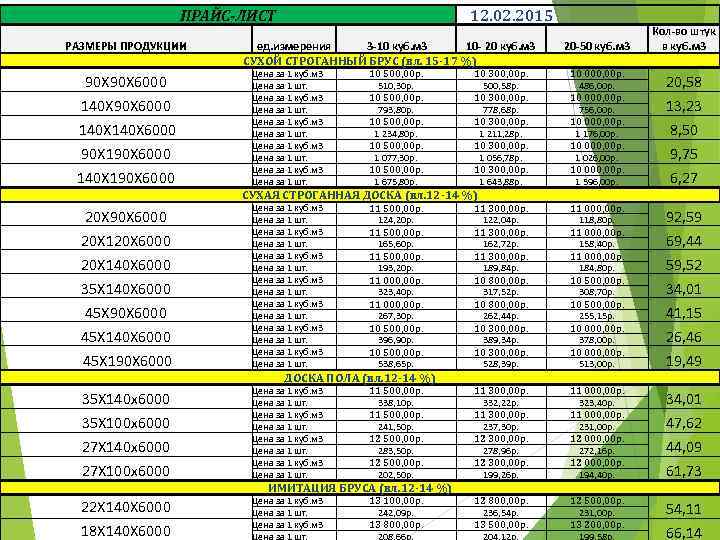 Вращение и перестановка циклов структуры — лучшая интерпретация концепции и теоремы теории групп. Ли [12] использовал кристаллографические символы для построения математической модели, описывающей n — куб порядка, основанный на теории групп точек. На основе математической модели создана компьютерная программа решения задачи о кубе.

Кубик Рубика рассматривается как абстрактный инструмент для изучения конкретных научных вопросов. В литературе [12] кубик Рубика использовался как модель для изучения кристаллической электронной дифракции, хаоса, генетики и других научных проблем. Американский математик Джойнер Дэвид [23] обсуждал теорию групп, полностью основанную на кубике Рубика и других подобных математических игрушках. Чен [24] изучал вращение кубика Рубика и определил понятие группы кубика Рубика.

В соответствии с законом вращения кубика многие свойства группы кубика Рубика описаны в системе теории групп. Кубик Рубика используется в качестве модели для описания основных частиц в физике.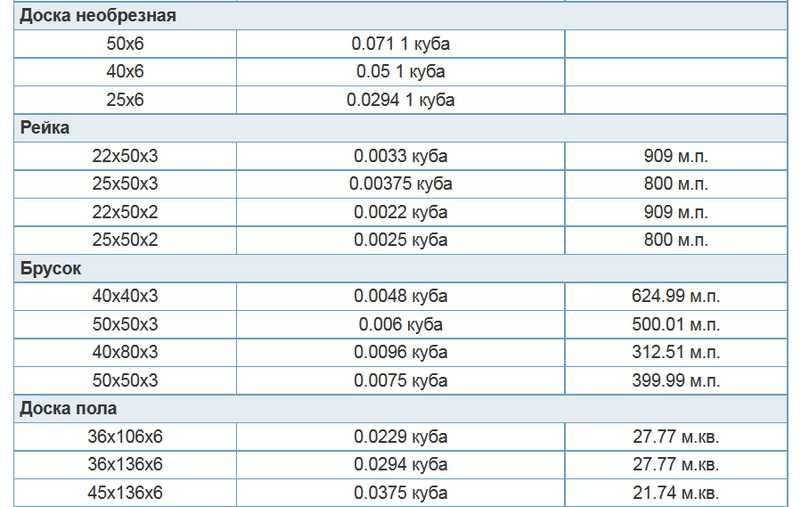 Кроме того, структура некоторых веществ в природе подобна структуре кубика Рубика, в том числе Ag/AgCl [25] и наноклетки TiO ₂ [26], как показано на рисунке 18.

Рисунок 18

TiO ₂ наноклетки со структурой Рубика

Изображение в полный размер

Кроме того, кубик Рубика также имеет некоторые применения в области психотерапии [27]. Кубик Рубика постепенно стал серьезно восприниматься в сфере образования, потому что он содержит богатые научные знания. В некоторых начальных и средних школах проводятся курсы математики на основе кубов, чтобы улучшить способность учащихся к обучению. Есть также некоторые релевантные исследования, показывающие, что использование «игровых кубиков» в качестве учебного пособия в занятиях по математике в начальной школе способствует стимулированию интереса учащихся к обучению и помогает учащимся мыслить абстрактно и развивать пространственные представления [28]. Кубик Рубика рассматривался как инструмент применения довольно сложной математики для создания некоторых алгоритмов решения [29]. ].

Алгоритм кубика Рубика

Кубик Рубика известен как классическая развивающая игрушка с уникальным шармом с момента его изобретения. От общего восстановления до быстрой скорости и минимального шага для восстановления, от искривления одной руки до восстановления вслепую [30], все больше и больше энтузиастов кубика Рубика и гонщиков увлекаются более сложными играми в кубик Рубика.

Существует множество видов кубиков Рубика. «Закон первого слоя» был предложен Дэвидом Сингмастером и используется большинством людей. Сначала восстановите верхний слой, затем восстановите средний слой и, наконец, восстановите нижний слой. Математик Конвей [31] из Кембриджского университета предложил шестиэтапный метод редукции снизу куба к середине, затем к вершине и постепенно от краев к угловым частям. Патрик [32] предложил метод шестигранной редукции: сначала восстанавливают угловые и краевые детали верхнего слоя, затем восстанавливают нижние угловые детали и, наконец, восстанавливают краевые детали среднего и нижнего слоев.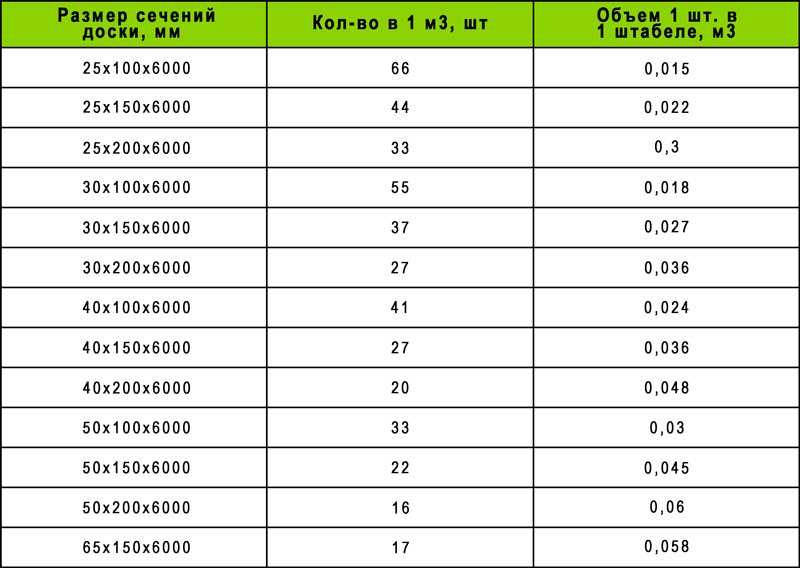 Джессика изобрела «Метод Фридриха», который используется большинством гонщиков для быстрого восстановления кубика Рубика. Этот метод широко используется, вдохновляет и влияет на исследователей кубиков и сыграл решающую роль в разработке кубика Рубика [33].

Алгоритм кубика Рубика также может быть решен компьютерным искусственным интеллектом. Ричард Э. Корф использовал метод «макрооператора» для решения алгоритма кубика Рубика с помощью компьютерной программы и получил полное описание процесса сокращения сторон куба [34]. Рокицкий и др. доказал, что максимальное количество ходов для решения куба равно 20 [35].

Применение кубика Рубика Характеристики

В последние годы, с развитием широкополосных сетей и наступлением информационной эры, безопасность данных и защита прав на неприкосновенность частной жизни становятся все более и более важными. Когда кубик Рубика остается в исходном состоянии, все участки каждой грани одного цвета и после нескольких вращений станут хаотичными. Восстановление кубика Рубика может следовать обратному шагу вращения или может следовать шагам разложения при восстановлении кубика Рубика. Таким образом, повернутую последовательность можно рассматривать как зашифрованный ключ для шифрования информации или сокрытия информации. В противном случае расшифровка очень затруднена [36].

В ссылках. [37,38,39], в качестве параметра преобразования кубика Рубика использовалась хаотическая последовательность, а метод шифрования изображения реализован алгоритмом циклического сдвига. В исх. [40] представлен эффективный метод шифрования изображений, основанный на принципе кубика Рубика с хаотической картой Бейкера. Предложенный метод повысил уровень безопасности метода шифрования кубика Рубика.

Кроме того, для нанесения водяных знаков на изображения был предложен алгоритм хаотического смешивания, основанный на концепции кубика Рубика [41]. Ссылка [42] использовали матрицу и трехмерную структуру эталона кубика Рубика, чтобы скрыть информацию изображений в градациях серого.

В арт. [43], Цай предложил мультиморфологическое сокрытие даты изображения на основе применения алгоритма кубика Рубика. Изображение можно разделить на 54 элемента и сформировать кубик Рубика. В общей сложности 54 элемента выбираются последовательно и преобразуются в 6 граней в соответствии с 6 гранями кубика Рубика путем присвоения порядкового номера, как показано на рис. 19 и рис. 20. Зашифрованные данные скремблируются с помощью алгоритма кубика Рубика.

Рисунок 19

Сопоставление кубика Рубика и изображения

Полноразмерное изображение

Рисунок 20

Соответствующий индекс кубика Рубика

Полноразмерное изображение

Алгоритм кубика Рубика применялся в схемах передачи конфиденциальной информации для шифрования информационного трафика по незащищенным физическим каналам [44]. Существует также облачный механизм защиты данных, основанный на алгоритме отпечатка пальца, который шифрует файл, управляя вращением кубика Рубика, которое зависит от значения признака отпечатка пальца пользователя [45].

Характеристики вращения и перестановки структуры кубика Рубика повышают защиту пароля от атак. Таким образом, кубик Рубика очень полезен в области шифрования и стал идеальной экспериментальной опорой для проверки того, может ли оператор робота соответствовать исходному стандарту.

В арт. [46] восстановление кубика Рубика использовалось в качестве трехмерной рабочей задачи для робота с различными датчиками (такими как зрение, сила, крутящий момент и тактильные датчики). Работоспособность контроллера системы управления роботом можно проверить с помощью операции восстановления кубика Рубика [47], как показано на рисунке 21, включая движение, ускорение, задержку и ориентацию робота [48].

Рисунок 21

Двуручная система, управляющая кубиком Рубика

Изображение в полный размер

Существует метод сборки кубика Рубика с помощью робота, основанный на неинвазивном интерфейсе мозг-компьютер без использования рук и с мыслью только о кубиках Рубика.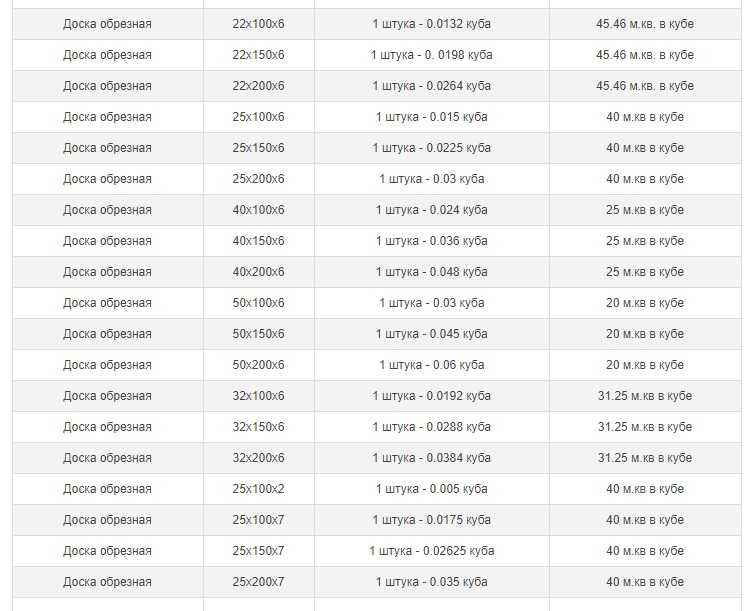 Вращение куба. Этот метод повышает скорость решения, а также помогает инвалидам, которые не могут собрать кубик Рубика руками [49].

В настоящее время, благодаря интеллектуальному развитию науки и техники, робот может успешно восстанавливать кубик Рубика, а это означает, что интеллектуальные технологии становятся все более и более зрелыми. Разработка интеллектуального робота, который может автоматически восстанавливать кубик Рубика после произвольного сбоя, включает в себя цифровую обработку изображений, компьютерное зрение, технологию распознавания образов, искусственный интеллект, организацию и другие технологические дисциплины. В процессе восстановления кубика Рубика может быть выявлена работоспособность робота, а также может быть отражено отсутствие механизма. Можно предложить соответствующий способ, чтобы вовремя компенсировать недостатки робота, и это будет способствовать развитию робота с более высоким интеллектом.

Появились некоторые концепции, связанные с механическим проектированием, а также были изобретены некоторые продукты, использующие характеристики конструкции кубика Рубика. Примеры включают новый парольный замок, состоящий из кубика Рубика с подбородком [50]. В исх. [51] был разработан метаморфический механизм, который использовал куб как платформу для работы машины и мог использоваться в мультиструктуре. Кроме того, есть некоторые идеи по применению куба в аэрокосмической отрасли, такие как комбинация структуры куба и спутника, использование куба-спутника для управления расположением куба и реконструкцией ориентации для выполнения различных задач [1]. 52]. Чжао предложил дизайн приложения деформируемого самолета для исследования дальнего космоса типа магического квадрата, применяя магические структурные особенности модульности и возможности вращения к космическому кораблю, так что каждая коробка куба имеет четкое разделение лаборатории, а затем путем сотрудничества для выполнить задание по исследованию дальнего космоса [53]. Вдохновленный вездесущей игрушкой Кубик Рубика, был предложен безаппаратный метод изготовления бумажных аналитических устройств [54].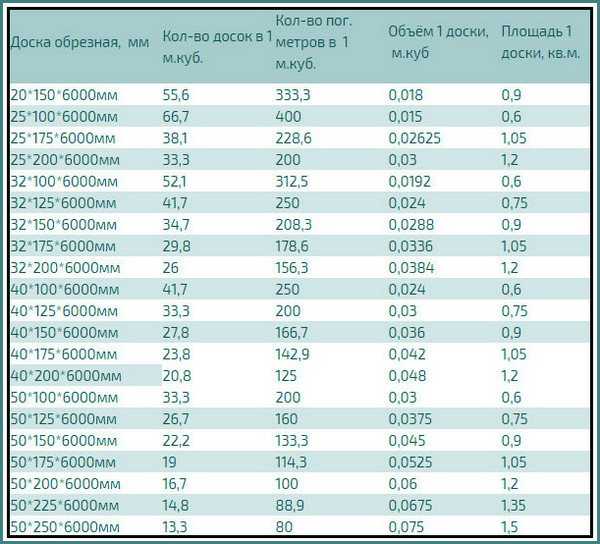

Применение кубика Рубика Структура и мышление в механизме

Кубик Рубика, «Хуаронгдао», изобретенный китайцами, и «Независимый бриллиант», изобретенный французами, известны как три главные интеллектуальные игрушки мира [55]. Хотя кубик Рубика был изобретен чуть более 40 лет назад, он пользуется популярностью у людей во всем мире, и все большее число энтузиастов и ученых увлекаются кубиком Рубика. Основная причина в том, что кубик Рубика содержит эзотерические математические принципы и всеохватывающую трансформацию, которая привлекает любопытных людей к изучению тайн кубика Рубика.

Эти исследователи изучили описание вращения кубика Рубика, изучили алгоритмы восстановления и математические принципы кубика Рубика, а также использовали кубик Рубика в качестве модели для изучения научных проблем в мультидисциплинарных областях. Как видно из приведенных выше исследований, с исследованием и применением кубика Рубика, это не только интеллектуальная игрушка. Он превратился из объекта исследования в объект значимости в междисциплинарных исследованиях.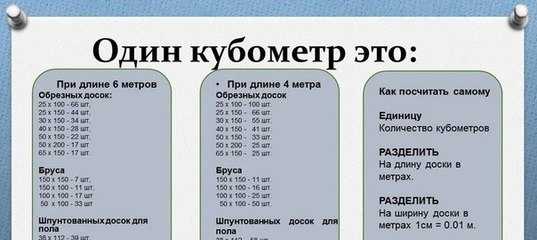 Эти исследования и приложения в основном основаны на абстрактных характеристиках структуры кубика Рубика. Исследования по изучению закона внутреннего механизма кубика Рубика только начались. Принцип механизма построения кубика Рубика еще предстоит глубоко изучить.

Устройство и механизм игрушки

Некоторые новые теории существующего механизма были вдохновлены изделиями ручной работы или изысканными игрушками и были обновлены в результате соответствующих исследований.

Вей [56] проанализировал степень свободы хромосферного механизма с помощью уравнения петлевого винта. В исх. В работе [57] степень свободы механизма магического шара анализировалась на основе теории структурной декомпозиции и системы эквивалентной спирали. Теория многопетлевого механизма сцепления была предложена путем изучения игрушек с характеристиками сцепления. На рисунке 22 показаны хромосферный механизм и механизм магического шара.

Рисунок 22

Игрушки с характеристиками сцепления

Изображение в полный размер

Дин [58,59,60] использовал куб змеи для изучения математического выражения составных элементов механизма, эквивалентной трактовки движения механизма, описания механизма интерференция движения и идентификация изоморфизма, а также определение последовательности реконфигурируемого механизма, который может достичь целевой конфигурации. В исх. [61] было рассчитано позиционное решение целевой конфигурации. Исследования змеиного куба обогатили теорию модульных реконфигурируемых механизмов, как показано на рис. 23.

Рисунок 23

Структура змеиного куба

Изображение в полный размер

Куо [62] проанализировал механизм реконфигурируемого куба, как показано на рисунке 24. Это соединение-головоломка, состоящее из восьми соединенных подкубов, и эквивалентно одиночному Петля 8R пространственная связь с восемью различными топологическими конфигурациями и изменяемой подвижностью.

Рисунок 24

Реконфигурируемый кубический механизм

Изображение полного размера

Сяо проанализировал структуру замков-головоломок с открытой замочной скважиной, которые широко использовались в древнем Китае. Замки-головоломки с открытой замочной скважиной, как показано на рисунке 25, представляют собой реконфигурируемые механизмы, которые имеют различные топологические структуры в работе [63].

Рисунок 25

Замок с открытой замочной скважиной

Изображение в полный размер

Dai et al. [64, 65] предложили теорию метаморфического механизма на основе исследований ремесел оригами. Это вызвало интерес научных кругов и стало одной из последних тем в области механики.

Метаморфический механизм имеет характеристики, включая переменную степень свободы и топологию, и может применяться в различных условиях эксплуатации. Такие механизмы могут подходить для неструктурированных сред, переменных условий и многозадачности [66]. Ли и Эрве предложили разрывной механизм связи свободы, который основан на принципе кубика Рубика и имеет свойство переменного числа стержней и степеней свободы [67].

При анализе кубика Рубика было установлено, что некоторые свойства механизма кубика Рубика аналогичны метаморфическим механизмам, а некоторые свойства аналогичны механизмам многоконтурной связи. Примеры включают характеристику связи внутреннего контура с кинематической цепью многоконтурного механизма связи, а также характеристику бифуркации движения изменения степени свободы и изменения движения после особого положения. Можно видеть, что кубик Рубика имеет множество характеристик механизмов и представляет собой комбинацию многих видов характеристик механизмов, но это не просто суперпозиция вышеперечисленных механизмов.

Структура кубика Рубика умная, простая, компактная и постоянно меняющаяся. В какой-то степени он выходит за рамки традиционных механизмов концепции топологии и общепринятых методов институционального проектирования. Кубик Рубика применялся в повседневной жизни, и ученые проводили исследования проблемы кубика в области механизма. Только глубокое изучение и анализ структуры куба может привести к систематическому построению теории топологии механизма кубика Рубика.

Обзор применения кубика Рубика в механизме

С постоянным повышением спроса на механические изделия классические механизмы переходят к современным сложным механизмам, которые изменили топологию с фиксированной на топологию с переменной и со слабой связи на сильную связь. Изменяемая топология и сильная связанность кубического тела постепенно привлекали внимание. По сравнению с параллельным механизмом и простым многоконтурным спаренным механизмом конструкция кубика Рубика имеет более высокую комплексную степень свободы, стойка конструкции кубика Рубика связана с рядом исполнительных органов, а связь между стержнем и стержнем прерывистая. Тем не менее, кубик Рубика имеет большой потенциал применения в промышленности благодаря своим особенностям, в том числе высокому использованию пространства, большому количеству комбинаций, сложной спортивной форме и многомодульной структуре.

Применение кубика Рубика в машиностроении имеет следующие три идеи:

(1)
Многосторонние эффекторы кубика Рубика и возможность перестановки и комбинирования могут быть применены к механическому дизайну. Механизм кубика Рубика можно использовать в качестве основной конструкции многофункциональных механических изделий. Использование вращения механизма куба может обеспечить желаемое положение или форму движения, так что разные концы привода могут выполнять задачу по порядку в определенном положении или заставлять разные концы привода работать вместе для выполнения задания. при упорядоченном сотрудничестве.
(2)
В соответствии с характеристиками кинетических пар структуры кубика Рубика, которые отличаются от обычной структуры, кинетические пары кубиков могут быть интегрированы в текущий промышленный механизм. Если такая умная конструкция сможет заменить сферический шарнир робота, то будет решена проблема небольшого угла поворота сферического шарнира, ограниченного механической конструкцией, что расширит рабочее пространство робота, особенно параллельного механизма. Если эту конструкцию можно применить к держателю станка или манипулятору механической руки, гибкость зажима и работы будет значительно улучшена.
(3)
Конструкция кубика Рубика занимает много места. Если эту характеристику можно применить к другим механическим изделиям, это будет способствовать процессу миниатюризации механических изделий.

Кроме того, с развитием мировой аэрокосмической промышленности будет появляться все больше и больше проектов по исследованию дальнего космоса. Некоторые особенности структуры кубика Рубика, включая модульность, вращающиеся, многофункциональные, многоцелевые и перерабатываемые функции, могут быть применены к конструкции космических кораблей или транспортных средств для исследования дальнего космоса.

Согласно приведенным выше идеям применения, применение кубической структуры также требует фундаментальных теоретических исследований. Движение продукта для достижения определенного направления предполагает исследование степеней свободы для достижения требуемой формы движения и конкретного состояния, связанного со структурным математическим выражением и метаморфическими свойствами. Есть некоторые проблемы с механизмом кубика Рубика, в том числе определенная степень гибкости, большое количество поверхностных контактов, количество направлений движения специальных мест и многое другое. Будут проведены последующие исследования по конкретным статическим характеристикам, трению, контролю и другим темам.

При дальнейшем изучении потенциальных применений кубика Рубика необходимо изучить проблемы механизма структуры кубика. Это может заложить теоретическую основу для применения кубического механизма и продвигать специальные кубические механизмы от обучающих игрушек до машин (таких как роботы, аэрокосмическая промышленность и т. д.).

Выводы

Существует множество разновидностей кубика Рубика. Были достигнуты некоторые успехи в теоретических исследованиях и приложениях. В этой статье систематически представлено происхождение и развитие кубика Рубика, проанализированы характеристики структуры и производительности кубика Рубика, а также рассмотрен исследовательский статус кубика Рубика, включая научные метафоры, алгоритмы восстановления и характерные приложения.

Внешние характеристики кубика Рубика изучались и применялись в междисциплинарных областях, поэтому одновременно следует исследовать принципы внутренней структуры кубика Рубика.

В этом документе описывается связь между кубиком Рубика и механизмом. Исследование кубика Рубика в области механизма все еще находится на начальной стадии. Следует изучить новые проблемы механизма кубика Рубика и сформировать системную теорию механизма кубика Рубика. Некоторые достижения исследования имеют определяющее значение в развитии механизма кубика Рубика в приложениях машиностроения.

Изучение механизма куба и содействие развитию структуры куба имеет большое значение. Топологическая теория кубического механизма еще нуждается в дальнейшем изучении. Можно полагать, что кубик Рубика будет иметь широкие перспективы для применения в машиностроении, основываясь на его исследовательском статусе и эффекте побочного эффекта в некоторых научных исследованиях, включая математику, физику, компьютеры и биологию.

Ссылки

D Gebhardt, G Hellings, WH Huang, et al. Куб . Нью-Йорк: Black Dog & Leventhal Publishers, 2009.
Т де Кастелла. Люди, которые все еще зависимы от кубика Рубика. Журнал BBC News. Би-би-си, 2014 [2018-05-30]. http://www.bbc.com/news/magazine-27186297.
Репортер Daily Mail. « Сведенный с ума» орех Рубика плачет, собирая кубик… после 26 лет попыток , 2009 г. http://www.dailymail.co.uk/news/article-1112396/Driven-mad-Rubiks-nut-weeps-solving -cube—26-years-trying.html.
В. Д. Стивен. Изобретение ХХ века: 100 изобретений, изменивших мир . Нью-Йорк: Издательство Нью-Йоркского университета, 2002.
. Google ученый
Т Джером. Кубик Рубика 25 лет спустя: Безумные игрушки, Безумные времена. Лондон: The Independent, 2007. https://www.independent.co.uk/news/science/rubiks-cube-25-years-on-crazy-toys-crazy-times-5334529.html.
Карлайл, П. Родни. Энциклопедия игр в современном обществе. Thousand Oaks: SAGE Publications Inc, 2009.
Европа. Интервью с Эрно Рубиком , 2016 г. http://www.create2009.europa.eu/ambassadors/profiles/erno_rubik.html.
Дж Ори. Как собрать кубик Рубика? , 2017. https://ourpastimes.com/do-beat-rubiks-cube-6508960.html.
Джей Ли. Сборка кубика Рубика для начинающих ., 2008 г. http://peter.stillhq.com/jasmine/rubikscubesolution.html.
Решатель кубика Рубика , 2016. https://rubiks-cube-solver.com.
Кубик Рубика: вопрос, ожидающий ответа , 2014 г. https://www.youtube.com/watch?v=W1K2jdjLhbo.
S C Li. Наука и культура в кубике Рубика . Пекин: Higher Education Press, 2015. (на китайском языке)
. Google ученый
Дж. Дж. Лю. Восточное зарождение комбинаторики. Журнал Северо-Западного университета (издание естественных наук) , 2001, 31 (5): 457–460. (на китайском языке)
MathSciNet Google ученый
С Банделоу. Внутри кубика Рубика и не только . Бостон: Издательство Birkhauser Boston Inc., 1980.
МАТЕМАТИКА Google ученый
А Лишевский. Вероятно, вы не проживете достаточно долго, чтобы собрать самый большой в мире кубик Рубика 22×22, 2016. .
Головоломки Грега. Мировой рекорд 33x33x33 Кубик Рубика, 2017. https://www.youtube.com/watch?v=NqJC3YxfcyM
Пазлы Шэн Шоу. Китайский магический куб . 2014 г. http://www.china-magic-cube.com/category/2.html.
Э. Рубик, Т. Варга, Г. Кери и др. Сборник кубиков Рубика. Нью-Йорк: Издательство Оксфордского университета. 1987.
Google ученый
R Ход. Нахождение общего количества допустимых перестановок кубика Рубика. Тронхейм: Тронхеймская Катедральская школа, 2010.
Google ученый
Дж. М. Ван, Дж. П. Фанг, Н. Чжан. Применение создания комбинаций в дизайне кубика Рубика. Арт Панорама . 2013(6): 105–105. (на китайском языке)
Google ученый
С. Дэвид. Заметки о волшебном кубике Рубика. Enslow Publishers, 1981.
А. Х. Фрей, С. Дэвид. Справочник по кубической математике. Издательство Энслоу, 1982.
Google ученый
Д Джойнер. Приключения в теории групп: Кубик Рубика, машина Мерлина и другие математические игрушки . Издательство Университета Джона Хопкинса, 2002.
МАТЕМАТИКА Google ученый
Дж Чен. Теория групп и кубик Рубика. ResearchGate, 2006.
Д. Хасан, В. Сумпун. Цветкоподобные микрокристаллы Ag/AgCl: синтез и фотокаталитическая активность. Химия и физика материалов , 2015, 159: 71-82.
Артикул Google ученый
G H Jiang, X H Wang, Y Zhou et al. Полые наноклетки TiO ₂ со структурой типа Рубика для высокоэффективных фотокатализаторов. Материалы Письма , 2012, 89: 59-62.
Артикул Google ученый
Дж. Д. Атен. Кубик Рубика: терапевтическая метафора. Журнал психологии и христианства , 2004, 23(3): 258.
Google ученый
J He, K Y Hu. Участие гида позволяет сублимировать мышление в математической деятельности — руководство преподаванием «Игры в кубик Рубика» на курсах математической деятельности в начальной школе. Образовательно-научный форум , 2011(2): 42-45. (на китайском языке)
Google ученый
Т. Дэвис. Обучение математике с кубиком Рубика. Математический журнал двухгодичного колледжа , 1982, 13 (3): 178–185. (на китайском)
Артикул Google ученый
Ю Чжэн. Теория кубика Рубика и ее приложения. Ханчжоу: Чжэцзянский университет, 2009 г. (на китайском языке)
Google ученый
Э. Берлекамп, Дж. Х. Конвей, Р. К. Гай. Способы выигрыша в математических играх . Лондон: Академическая пресса. 1982.
МАТЕМАТИКА Google ученый
Б Патрик. Можно сделать куб . Лондон: Книги тупиков. 1981.
Google ученый
Дж. Палмер. Разгадываем последнюю загадку кубика Рубика. New Scientist , 2008, 199(2668): 40-43.
Артикул Google ученый
Р Е Корф. Обучение решению задач путем поиска макрооператоров . Расширенный паб Питман. Программа, 1985.
T Rokicki, H Kociemba, M Davidson, et al. Диаметр группы кубиков Рубика равен двадцати. Журнал SIAM по дискретной математике , 2013, 27(2): 1082-1105.
MathSciNet Статья МАТЕМАТИКА Google ученый
ХБ Ма, ЛХ Лю. Разработка алгоритма перестановки кубика Рубика на основе хаоса. Вычислительная техника и приложения , 2006, 42(12): 138-140. (на китайском)
Google ученый
Л. Чжан, С. М. Цзи, И. Се и др. Принцип алгоритма шифрования изображений на основе преобразования магического куба. Конспект лекций по информатике , 2005, 3802: 977-982.
Артикул Google ученый
Дж. Шэнь, С. Джин, С. Чжоу. Алгоритм шифрования цветного изображения, основанный на преобразовании магического куба и модульной арифметической операции . Конспект лекций по информатике , 2005, 3768: 270-280.
Артикул Google ученый
Г. Дж. Бао, Дж. И. Ши-Мин, Дж. Б. Шен. Преобразование магического куба и его применение в шифровании цифровых изображений. Компьютерные приложения, 2002, 26(1): 7-22. (на китайском языке)
Google ученый
Л. Л. Чжао, З. Л. Фан, З. К. Гу. Новый алгоритм скремблирования и шифрования цифровых изображений, основанный на преобразовании магического куба. Журнал оптоэлектроники Laser , 2008, 19(1): 131–134. (на китайском языке)
К.А. Абита, П.К. Бхаратан. Безопасная связь на основе алгоритма кубика Рубика и хаотической карты пекарей. Procedia Technology , 2016, 24: 782-789.
Артикул Google ученый
E Йен, L H Лин. Технология водяных знаков кубика Рубика для изображений в градациях серого . Экспертные системы с приложениями , 2010, 37(6): 4033-4039.
Артикул Google ученый
К. Л. Цай, К. Дж. Чен, В. Л. Хсу. Мультиморфологическое сокрытие данных изображения на основе применения алгоритма Кубика Рубика. 2012 Международная Карнаханская конференция IEEE по технологиям безопасности , 2012: 135–139.
Google ученый
Дж.Л. Ли, Г.Л. Хуо, Б. Лю. Схема передачи конфиденциальной информации на основе алгоритма магического куба в автоматизированном согласовании доверия. Журнал компьютерных приложений , 2011, 31(4): 984-988. (на китайском языке)
Артикул Google ученый
Х. Ву, Дж. Л. Фан, Дж. Х. Лю. Механизм защиты данных облачного хранилища на основе алгоритма куба отпечатков пальцев. Наука о телекоммуникациях , 2014, 30(11): 110–115. (на китайском языке)
Google ученый
В Шинкевич. Планирование бимануальной манипуляции на основе навыков . Журнал телекоммуникаций и информационных технологий , 2012, 2012(4): 54-62.
Google ученый
С. Зелински, М. Станиак, В. Чаевски и др. Кубик Рубика в качестве эталона, подтверждающего MRROC++ как инструмент реализации для систем управления сервисными роботами. Промышленный робот , 2007, 34(5): 368-375.
Артикул Google ученый
С Копачи. Интерактивная визуализация в 3D. Журнал физиологии , 2012, 384(1): 671-690.
Google ученый
М. Р. Далири, Х. Самади. Соберите кубик Рубика с роботом на основе неинвазивного компьютерного интерфейса мозга. Иранская конференция по интеллектуальным системам (ICIS) 2014 г. , 2014 г.
X X Мяо. Кубик Рубика для упаковки: CN, 201510159029.9. 2015-04-07. http://www.patexplorer.com/patent/view.html?patid=CN201510159029.9&sc=&q=%E7%94%A8%E4%BA%8E%E5%8C%85%E8%A3%85%E7%89%A9%E7%9A%84%E9%AD%94%E6%96%B9&fq=&sort=&sortField= &page=1&rows=10#1/CN201510159029.9/detail/abst. (на китайском языке)
Р. Г. Ван, Ю. Ф. Ляо, Ч. Чжан. Краб-машина для обхода препятствий с метаморфическим механизмом: CN: 201510119249.9. 2015-06-17. http://www.patexplorer.com/patent/view.html?patid=CN201510119249.9&sc=&q=%E4%B8%80%E7%A7%8D%E5%8F%98%E8%83%9E%E6 %9C%BA%E6%9E%84%E5%BC%8F%E5%8F%AF%E8%B6%8A%E9%9A%9C%E6%9C%BA%E5%99%A8%E8%9F%B9&fq=&sort=&sortField=&page=1&rows=10#1/CN201510119249.9/deta. (на китайском языке)
BJ Cui. Спутник-куб и метод его проектирования: CN, 2013107194458.8. 2014-04-16. http://www. patexplorer.com/patent/view.html?patid=CN201310719458.8&. (на китайском языке)
Б. Х. Чжао, С. И. Гао, Дж. Н. Чжан и др. Самолет для исследования дальнего космоса по типу кубика Рубика. Технологические инновации и применение , 2014(24): 61–63. (на китайском)
Google ученый
Н Фу. Использование кубика Рубика для непосредственного производства бумажных аналитических устройств для количественных анализов на основе аптамеров по месту оказания медицинской помощи. Биосенсоры и биоэлектроника , 2017, 96: 194–200.
Артикул Google ученый
Ю Чен, Л Цзян. Анализ применения кубика Рубика в обучении . Китайское электроэнергетическое образование , 2012 (8): 88–89.. (на китайском языке)
Google ученый
G Wei, X Ding, J S Dai. Подвижность и геометрический анализ мяча Хобермана Switch-Pitch Ball и его варианта. Журнал механизмов и робототехники , 2010, 2(3): 191-220.
Артикул Google ученый
Дж. С. Дай, Д. Ли, К. Чжан и др. Анализ подвижности сложноструктурированного шара на основе декомпозиции механизма и анализа эквивалентной винтовой системы. Механизм и теория машин , 2004, 39 (4): 445–458.
Артикул МАТЕМАТИКА Google ученый
Х Л Дин, С Н Лю, И Ян. Теория трансформации конфигурации из модульного реконфигурируемого механизма цепного типа-Змейка Рубика. 13-й Всемирный конгресс по механике и машиноведению , Мексика, Гуанахуато: IFToMM, 2011: A12_380.
X L Ding, S N Lu. Теория реконфигурации модульного реконфигурируемого механизма, основанная на анализе змеиного куба. Журнал машиностроения , 2012, 48 (11): 126–135. (на китайском языке)
Артикул Google ученый
X Дин, С Лю. Фундаментальная теория реконфигурации модульных реконфигурируемых механизмов цепного типа . Механизм и теория машин , 2013, 70 (Приложение C): 487–507. (на китайском языке)
C Wang, J J Xu. Алгоритм нахождения трехмерных путей S-образного интеллектуального магического квадрата. Компьютерные знания и технологии , 2008, 1(4): 686–690.
Google ученый
Ч. Куо, Дж. В. Су. Анализ конфигурации класса реконфигурируемых кубических механизмов: мобильность и изоморфизм конфигурации. Механизм и теория машин , 2017, 107: 369–383.
Артикул Google ученый
К. Х. Сяо. О структурном анализе замков-головоломок с открытой замочной скважиной в Древнем Китае. Механизм и теория машин , 2017, 118: 168-179.
Артикул Google ученый
Дж. С. Дай, Дж. Р. Джонс. Подвижность в метаморфических механизмах складно-разборного типа. Journal of Mechanical Design , 1999, 121(3): 375-382.
Артикул Google ученый
Д.Л. Ли, Ч.Х. Чжан, Дж.С. Дай. Обзор и перспективы метаморфического механизма. Журнал машиностроения , 2010, 46(13): 14-21. (на китайском языке)
Артикул Google ученый
Департамент инженерии и материаловедения, Национальный фонд естественных наук Китая. Отчет об исследовании стратегии развития дисциплин (2011–2020 гг.): Машиностроение . Пекин: Science Press Ltd, 2010. (на китайском языке)
C C Lee, J M Herve. Разрывная подвижность четырехзвенных механизмов с вращательной, призматической и цилиндрической парами через групповую алгебраическую структуру множества перемещений. 8-я Международная конференция по теории машин и механизмов , Чехия: Либерец Эльсмере, 2001: 5–7.

Ссылки на скачивание

Вклад авторов

D-XZ и ZH отвечали за все испытание; ML и J-JW написали рукопись; Y-LH и W-JL помогали с отбором проб и лабораторными анализами. Все авторы прочитали и одобрили окончательный вариант рукописи.

Информация для авторов

Да-Син Цзэн, 1978 г.р., в настоящее время профессор в 9 лет0401 Яншаньский университет, Китай. Он получил степень доктора философии в области мехатроники в Yanshan University, China , в 2008 году. Его исследовательские интересы включают теорию механизмов и машин, параллельные механизмы, синтез типов и обработку изображений.

Мин Ли, 1992 года рождения, в настоящее время является кандидатом в магистратуру в Yanshan University, Китай. Его исследовательские интересы включают анализ кубика Рубика, параллельный механизм и синтез типов.

Хуан-Хуан Ван, 19 г. р.91, в настоящее время является кандидатом в мастера в Yanshan University, Китай . Ее исследовательский интерес — параллельный механизм.

Юй-Лей Хоу, 1980 г.р., в настоящее время является профессором Университета Яньшань, Китай . Его исследовательские интересы включают параллельный механизм, многоосевой датчик силы, бионику робота-человека и т. д.

Вэнь-Хуан Лу, 1983 г.р., в настоящее время является доцентом Yanshan University, China . Ее исследовательские интересы включают параллельный механизм, синтез типов и т. д.

Чжэнь Хуан, 1936 года рождения, в настоящее время является профессором и научным руководителем кандидата наук в Школе машиностроения Университета Яньшань, Китай . Его основные исследовательские интересы включают параллельный робот, синтез типов и топологию.

Конкурирующие интересы

Авторы заявляют об отсутствии конкурирующих интересов.

Финансирование

При поддержке Национального фонда естественных наук Китая (грант № 51775473), Провинциального фонда естественных наук провинции Хэбэй Китая (грант № E2018203140), Проекта по строительству системы провинции Хэбэй в рамках Программы технологических инноваций (грант № 182419)05Д).

Примечание издателя

Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.

Информация об авторе

Авторы и организации

Школа машиностроения, Университет Яньшань, Циньхуандао, 066004, Китай
Да-Син Цзэн, Мин Ли, Хуан-Жуан Ван, Луан-Лей-Джу, Юй-Лей-Джу & Чжэнь Хуан

Авторы

Да-Син Цзэн
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Ming Li
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Juan-Juan Wang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Yu-Lei Hou
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Wen-Juan Lu
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Zhen Huang
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar

Автор, ответственный за корреспонденцию

Чжэнь Хуанг.

Права и разрешения

Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 4.0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение, и воспроизведение на любом носителе, при условии, что вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения.

Перепечатки и разрешения

Об этой статье

Учебник по сборке кубика Рубика

Сборка кубика Рубика!

Легко, когда знаешь как.

Введение

Узнайте, как собрать кубик Рубика с помощью простых инструкций и интерактивных демонстраций.

Кубик Рубика может показаться почти невозможным, когда вы впервые начинаете с ним играть. Разместить первые несколько кусочков достаточно легко, но вскоре вы обнаружите, что ничего не можете сделать, не набивая другие области. Когда вы знаете шаги и вооружены правильными алгоритмами, это на самом деле довольно просто. На следующих страницах вы познакомитесь с простым и легким в применении набором алгоритмов (предварительно организованных шагов), которые помогут решить куб. (Кубик Рубика — это продукт, созданный компанией Rubik’s Brand Ltd. Это просто руководство по его сборке и никоим образом не связано с компанией.)

Outline

Этот учебник по кубам разделен на 5 разделов. Остальная часть этой страницы знакомит вас с нотацией куба и знакомит с вашим кубом. Остальные страницы работают на решение куба.

Продолжайте читать ниже, чтобы начать работу, или перейдите к одному из следующих разделов.

1. Соберите белый крест
2. Решите белые углы
3. Решить второй слой
4. Решите желтый крест
5. Решить последний слой
Задачи с узорами. Просто для развлечения, посмотрите, сможете ли вы создать эти узоры из кубов (а затем бросьте вызов другим, чтобы решить их интуитивно).
Шпаргалка — все алгоритмы на одной странице для удобства.
Симулятор куба — полезен для обучения сборке куба.

На каждом шаге руководства перечислены алгоритмы и даны подробные пояснения. Если вы не хотите читать объяснения, вы можете их пропустить.

Знакомство с кубиком

Каждый берет кубик Рубика по-своему. Некоторые люди довольно быстро поймут, как манипулировать фигурами. Другим потребуется немного больше времени. С практикой манипулирования фигурами станет легче, и вы начнете понимать, как определенные ходы приводят к определенным результатам. То, что на первый взгляд кажется просто слепым следованием алгоритмам, начнет обретать смысл, и вы начнете модифицировать алгоритмы для создания ярлыков.

Перед тем, как мы начнем собирать куб, может быть полезно получить представление о том, как ведет себя куб. Хорошим начальным упражнением является работа над сборкой только одной грани куба. Не волнуйтесь, если квадраты, примыкающие к этой грани, не выстраиваются правильно, просто работайте над решением одной грани. Вы должны быть в состоянии сделать это интуитивно (то есть без использования предопределенных алгоритмов). Это помогает понять, как части перемещаются и как можно расставлять их по местам, не затрагивая других. Вы должны потренироваться держать куб двумя руками, делая это и манипулируя кубом обеими руками. В качестве дополнительной задачи посмотрите, сможете ли вы собрать грань куба одной рукой.

Кубики

Кубик Рубика состоит из трех различных типов деталей.

	Угловые элементы — 8 угловых элементов. Они имеют 3 панели и могут быть в любой из 3 ориентаций в каждом положении.
	Кромки — 12 кромок. У них есть 2 панели, и каждая может быть в любой из 2 ориентаций.
	Центральные элементы — 6 центральных элементов. У каждого из них есть только одна панель, поэтому они могут быть в одной ориентации. Эти части также определяют шесть граней куба. например. лицо с синей центральной частью — синее лицо.

Все это дает 26 частей, составляющих куб с 54 панелями на этих частях. Это приводит к ошеломляющим 43, 252, 003, 274, 489, 856, 000 возможных комбинаций . Несмотря на это большое количество, группа или исследователи с кучей свободного вычислительного времени на самом деле разработали оптимальное решение для каждой из этих комбинаций, установив, что максимальное необходимое количество ходов (см. Ниже) для решения любого куба составляет 20 ходов. Практически все эти комбинации требовали различных алгоритмов для оптимального решения, и мы не собираемся предлагать вам запоминать такое количество комбинаций и соответствующих алгоритмов.

Вместо этого мы познакомим вас с алгоритмами для начинающих. Они включают в себя более 20 ходов, но гарантированно решают любую комбинацию. В этом сила хорошо продуманных алгоритмов, они могут быть очень гибкими в том, что они могут решать. Вот почему этот учебник по кубику Рубика находится на веб-сайте с учебными пособиями по ИТ. Научиться собирать кубик Рубика — отличный способ изучить, как мы можем эффективно настраивать процессы, чтобы принимать широкий спектр возможных входных данных и надежно преобразовывать их в заданные выходные данные.

Обозначение куба

Для решения куба необходимо следовать набору алгоритмов. Чтобы проиллюстрировать алгоритмы, мы будем использовать обозначение куба, как указано ниже. (Существует несколько вариантов обозначения куба, но как только вы узнаете один, приспособиться к другим довольно легко.)

Каждое из этих движений представляет собой поворот соответствующих фигур на 90 градусов. У каждого хода также есть соответствующий противоположный ход, который обозначается апострофом (‘).

U — Поверните верхнюю (вверх) сторону по часовой стрелке.

U’ — Поверните верхнюю (вверх) сторону против часовой стрелки.

D — Поверните нижнюю (вниз) сторону по часовой стрелке.

D’ — Поверните нижнюю (вниз) сторону против часовой стрелки.

R — Поверните правую грань по часовой стрелке.

R’ — Поверните правую сторону против часовой стрелки.

L — Поверните левую сторону по часовой стрелке.

L’ — Поверните левую сторону против часовой стрелки.

F — Повернуть переднюю грань по часовой стрелке.

F’ — Поверните переднюю панель против часовой стрелки.

B — Поверните заднюю сторону по часовой стрелке.

B’ — Поверните заднюю сторону против часовой стрелки.

M — Поверните вертикальный срез по часовой стрелке.

M’ — Поверните вертикальный срез против часовой стрелки.

E — Поверните горизонтальный срез по часовой стрелке.

E’ — Поверните горизонтальный срез против часовой стрелки.

S — Поверните верхний срез по часовой стрелке.

S’ — Поверните верхний срез против часовой стрелки.

Не беспокойтесь о попытках запомнить все это. Изображения, а также моделирование будут использоваться вместе с обозначениями при объяснении алгоритмов.

Часто просмотр ходов облегчает их понимание, поэтому вот куб, где вы можете увидеть каждый ход в действии.

Теперь вы готовы. Вы можете погрузиться в Шаг 1 — Решение белого креста или продолжить чтение ниже, если вам интересно.

Советы и рекомендации

Нередко вы чувствуете себя немного подавленным, когда впервые начинаете учиться собирать кубик Рубика. Со временем и практикой это быстро пройдет. Вот несколько советов и советов, которые помогут вам на пути к овладению кубом.

Просто делайте понемногу каждый день — если вы начинаете расстраиваться, оставьте это на некоторое время и вернитесь на следующий день. Некоторое время может помочь прояснить ситуацию.
Повторение — это хорошо — первые несколько раз, когда вы повторяете алгоритм шага, вам, вероятно, придется следовать руководству. Но скоро вы начнёте это вспоминать и сможете делать это самостоятельно. Повторение укрепит мышечную память, поэтому вам больше не нужно сознательно думать о выполнении этого шага. Это освободит ценные ресурсы вашего разума, которые вы сможете посвятить работе над следующим шагом.
Смешайте это — Соберите куб несколько раз, используя учебник в качестве справочного материала, затем сделайте несколько шагов, которые вы можете запомнить сами.
Во время обучения вы будете много раз ошибаться и забивать кубик. Если это произойдет, не беспокойтесь, вы можете попытаться отменить свои ходы и попробовать еще раз. Часто вы не помните, какие ходы вы на самом деле сделали, и просто еще больше запутаетесь, пытаясь отменить их. Не беспокойтесь, просто начните снова. Это хорошая практика.
Эксперимент — Алгоритмы для каждого шага сосредоточены на размещении определенных фигур. Они также будут перемещать другие фигуры по кубу. При изучении нового алгоритма найдите время, чтобы посмотреть на другие части вашего куба и на то, как они перемещаются. Это поможет вам лучше понять, как работает алгоритм, а также может привести к сокращению пути.

Сокращение времени

Начнем с того, что вам понадобится совсем немного времени, чтобы собрать кубик Рубика. С практикой это можно сделать менее чем за минуту. Вот несколько советов, которые помогут в этом:

Делайте движения пальцами, а не скручивая запястья. Это позволит вам делать движения намного быстрее и соединять движения вместе в быстрой последовательности.
Получите кубик скорости (см. ниже). Они позволяют вам крутить детали намного проще, чем стандартный кубик Рубика, и это также поможет сократить ваше время.
Изучите зеркальные отражения алгоритмов. Большинство алгоритмов можно сделать в зеркальном отображении и часто это позволяет более эффективно разместить фигуру.
Научитесь выполнять алгоритмы на лицах, отличных от того, которое обращено к вам. Это сократит время, затрачиваемое на переворачивание куба, чтобы получить правильную грань перед вами, и немного сократит ваше время.
Практика, практика, практика. Это, безусловно, лучший способ стать лучше, и многие из вышеперечисленных советов начнут происходить естественным образом с практикой.

Какой куб мне взять?

Стандартный кубик Рубика может легко стать довольно жестким, и его будет трудно поворачивать. Это может нарушить ваш поток и заставить работать с алгоритмами гораздо больше концентрации. На рынке есть много кубов других брендов, многие из которых продаются как Speed Cubes . Бренд Rubiks также продает один из них. У них часто есть детали с закругленными краями, которые обеспечивают более плавное вращение деталей. Вы также можете получить хороший скоростной куб очень дешево. Мой совет, чтобы получить один из них для гораздо лучшего опыта. Я не буду перечислять какие-либо конкретные сайты, на которых их можно купить. Выполните поиск в Google, и вы найдете множество розничных продавцов, продающих их.

Концепция раскрашенного куба, хитрости и ярлыки — Hitbullseye

В этой статье мы изучим концепцию разрезания куба или разрезания нарисованного куба. При решении этих вопросов наиболее важной частью является визуализация куба. Нарезка кубиком – важная концепция, так как вопросы по этой теме часто задают на ряде конкурсных экзаменов.

Предлагаемое действие

БЕСПЛАТНЫЕ живые мастер-классы от нашего Звездного факультета с более чем 20-летним опытом. Зарегистрируйтесь сейчас

Давайте сначала изучим некоторые основные термины, например, грань , вершина и ребро куба.

В кубе 6 граней, 8 вершин и 12 ребер. Вершина означает углы, а край означает сторону.

Как правило, вопросы из этой темы относятся к типу, в котором куб со стороной, измеряемой единицей измерения «x», окрашивается на всех гранях и разрезается на более мелкие кубики со стороной, измеряемой единицей измерения «y». Затем вам нужно найти количество кубиков, имеющих n окрашенных граней.

Первое, что вам нужно выяснить, это количество меньших кубиков. Для этого вы смотрите на одно конкретное ребро большого куба и выясняете, сколько меньших кубов может в него поместиться. Это будет х/у. Таким образом, количество меньших кубиков будет (x/y) ³ .

Поскольку все меньшие кубики будут иметь хотя бы одну грань, обращенную внутрь, т. е. не на поверхность исходного куба, следовательно, ни у одного из меньших кубов не будут закрашены все грани. Далее, поскольку максимальное количество граней большего куба, пересекающихся в одной точке, равно 3 (по углам), следовательно, меньшие кубы могут иметь максимум 3 окрашенные грани.

Итак, количество меньших кубов с 3 окрашенными гранями = Количество углов большего куба = 8 (всегда), при условии, что ни одна из граней большего куба не осталась неокрашенной.

Применим эту теорию к заданным вопросам.

Примеры вопросов по резке куба

Пример 1: Куб со стороной 6 см окрашен в красный цвет со всех граней, а затем разрезан на более мелкие кубики по 1 см каждый. Найдите общее количество меньших кубиков, полученных таким образом.

Решение:

Как объяснялось выше, количество меньших кубиков = (6/1) ³ = 216 меньших кубиков.
(Здесь x=6 и y=1)

Пример 2: В приведенном выше примере у скольких кубов будут окрашены три грани?

Решение: Как объяснялось выше, только угловые кубы, то есть 8 кубов в углах исходного куба, будут иметь три окрашенные грани. Следовательно, ответ будет только 8.
Чтобы найти количество меньших кубов, у которых окрашены только 2 грани, нужно рассмотреть кубы, где сходятся 2 грани большего куба, т. е. ребра. Помните, что сюда входят и кубики, находящиеся в углах, поэтому вам нужно удалить эти 2 кубика из числа кубиков на каждом ребре.

Пример 3: В приведенном выше примере у скольких кубов будут окрашены только две грани?

Решение: Как обсуждалось выше, только кубы на краю большего куба могут иметь две окрашенные грани.
Большой куб имеет ребро 6 см, а меньший куб имеет ребро 1 см. Значит, на каждом ребре по 6 кубиков. Однако вам нужно учитывать только 4 средних куба, так как 2 куба в каждом углу будут иметь 3 окрашенные грани.
Значит, на каждом ребре по 4 таких кубика. Так как ребер 12, то будет 4*12 = 48 кубиков

Пример 4: В приведенном выше примере у скольких кубов будет только одна грань и ни одна грань?

Решение: Как обсуждалось выше, только у кубов на грани большего куба может быть только одна окрашенная грань. Так как больший куб имеет ребро 6 см, а меньший куб имеет ребро 1 см, следовательно, если вы посмотрите на одну из граней большего куба, вы увидите 6 * 6 = 36 кубов. Из них исключите кубики, лежащие на ребрах, так как у них две или более граней окрашены. Таким образом, на каждой грани исходного куба будет 4 * 4 = 16 кубов с окрашенной только одной гранью.
Поскольку таких граней 6, количество таких меньших кубиков будет 16*6 = 96.

Наконец, количество кубиков, не имеющих окрашенных граней, можно найти, вычитая сумму окрашенных кубиков из общего количества кубиков. кубики меньшего размера. Следовательно, искомый ответ 216 – (8 + 48 + 96) = 64 куба.

Пример 5: Куб со стороной 12 см каждая. Он окрашен в красный цвет на двух противоположных гранях, в синий цвет на другой паре противоположных граней, в черный цвет на еще одну грань и одна грань остается неокрашенной. Затем его нарезают более мелкими кубиками по 1 см каждый. Ответьте на следующие вопросы:

Количество меньших кубиков, у которых окрашены три грани.
Количество меньших кубиков, у которых окрашены две грани.
Количество меньших кубиков, окрашенных с одной стороны.
Количество меньших кубов с нулевой гранью.

Решение:

Общее количество кубиков = (12*12*12)/(1*1*1)=1728
Для куба со всеми окрашенными сторонами у нас есть 8 кубов с 3 окрашенными сторонами. Но здесь у нас 1 сторона не окрашена. Следовательно, у нас будет всего 4 кубика с 3 окрашенными сторонами. Остальные 4 кубика будут окрашены только с двух сторон.
На 2 стороны окрашены, ищем края.
У куба 12 ребер.
8 ребер, каждое ребро, состоящее из 10 кубов, будет окрашено с двух сторон. (4 края неокрашенной стороны не учитываются).
Мы также включим эти 4 кубика (которые мы не учитывали при подсчете 3-х цветных сторон, т.к. у них 2 окрашенные стороны) неокрашенная сторона).
Следовательно, всего кубиков с 2 окрашенными сторонами = 8*10 + 4= 84 кубика.
Для 1 окрашенной стороны ищем грани куба.
Куб имеет 6 граней.
5 граней, каждая из которых имеет (12-2)*(12-2) = 100 кубов, будет окрашена с одной стороны.
Нам нужно включить те кубики на ребрах, которые связаны с неокрашенной гранью.
10 кубиков на каждом из этих ребер будут окрашены с одной стороны.
Таким образом, общее количество кубиков с 1 окрашенной стороной = 5*100 + 4*10 = 540 кубиков.
Согласно формуле, кубы без окрашенной стороны = (12-2) ³ = 1000.
Но мы должны включить кубики и с неокрашенной стороны. Это будет 10*10=100
Итак, общее количество неокрашенных кубиков= 1000+100=1100.

Сокращенные формулы

Для куба со стороной n*n*n, окрашенного со всех сторон, который равномерно разрезан на более мелкие кубики размерности 1*1*1,
Количество кубиков с окрашенной стороной 0= (n-2) ³
Количество кубиков с окрашенной 1 стороной =6(n — 2) ²
Количество кубиков с 2 окрашенными сторонами = 12(n-2)
Количество кубиков с 3 окрашенными сторонами = 8 (всегда)
Для прямоугольного параллелепипеда размерности a*b*c, окрашенного со всех сторон и разрезанного на меньшие кубики размерности 1*1*1,
Количество кубиков с окрашенной стороной 0= (a-2) (b-2) (c-2)
Количество кубиков с окрашенной 1 стороной =2[(a-2) (b-2) + (b-2)(c-2) + (a-2)(c-2) ]
Количество кубиков с 2 окрашенными сторонами = 4(a+b+c -6)
Количество кубиков с 3 окрашенными сторонами = 8

БЕСПЛАТНЫЕ электронные книги

Получите доступ к тщательно отобранным академическими экспертами электронным книгам для сдачи конкурсных экзаменов. Загрузить сейчас

Ключ Обучение:

Подводя итог, количество трехгранных закрашенных кубов можно найти с помощью вершин, двухгранных закрашенных с помощью ребер и одногранных закрашенных с помощью граней. Используя это обучение, мы можем даже решать сложные вопросы по резке куба, например, куба, окрашенного в разные цвета.

Страница не найдена – Национальный музей математики

Не найдено

К сожалению, эта страница не найдена.

Возвращение домой

В этом изящно кратком стихотворении Таис Эстрада-Нуньес начинает со слов «Одно семя плюс одно семя — два семечка», и вскоре мы улетаем (да и расположение самого стихотворения выглядит так, будто оно улетает на странице). Общий эффект стильный, с оттенками тонкости и глубины.

Нажмите здесь, чтобы прочитать стихотворение.

Используя тени самолета в качестве примера, иллюстрированное эссе Раунака Банерджи предлагает долгожданное введение в анализ главных компонентов, метод уменьшения размерности в науке о данных, а затем расшифровывает жаргон, который часто затрудняет понимание этого статистического метода.

Щелкните здесь, чтобы прочитать его эссе.

Анжела Ву получила поощрительный приз за напряженный трейлер фильма об особых параллелограммах: прямоугольниках, ромбах и квадратах. Это забавное и хорошо отредактированное видео, которое будет иметь широкую популярность.

Нажмите здесь, чтобы посмотреть видео

В этой впечатляющей коллекции записанных на видео лекций о математике нейронных сетей, глубоком обучении и искусственном интеллекте Адам Дхалла придерживается старой школы, стоя перед доской и используя цветные маркеры, но модернизирует классический стиль, добавляя полезные временные метки. в описании видео. Судьи также восхищались его сценическим присутствием, чистым голосом и качеством производства видеороликов.

Нажмите здесь, чтобы посетить сайт Адама

Сайт Аруши Джа «Вокруг Кенигсберга» посвящен комбинаторике и оживлен красочными оригинальными рисунками Аруши. Зрителей привлечет изложение на веб-сайте таких интересных тем, как семь мостов Кенигсберга (основная проблема в развитии теории графов), а также история и рассуждения о магических квадратах.

Нажмите здесь, чтобы посетить веб-сайт.

В эссе Карима Джабера о головоломке 15 экспозиция строится от конкретного к общему и мягко знакомит читателя с этой классической головоломкой, а также с более широкими методами решения проблем. К концу становится ясно, что эта головоломка на самом деле представляет собой тематическое исследование теории групп о перестановках. Судьи сочли, что работа Карима особенно подходит для студентов, серьезно интересующихся математикой.

Нажмите здесь, чтобы прочитать эссе.

Поэма Уайета Ренвика интригующе двусмысленна и открыта для интерпретаций: некоторые судьи прочитали ее как любовную поэму, которая подмигивает читателю с помощью математических понятий и языка, в то время как другие увидели в ней поэтическую анимацию человеческих отношений, рассматриваемых как график функции. В любом случае, благодаря этому математика и поэзия кажутся более доступными для учащихся, которых в противном случае эти предметы не привлекли бы.

Нажмите здесь, чтобы прочитать стихотворение.

Судьи были поражены энергией и чувством юмора в работе Гриффина Хона «Случайные прогулки»! Это видео понравится детям всех возрастов, и оно отлично передает волнение, важность и универсальность случайных блужданий. Тема случайных блужданий возникает во многих разделах математики и имеет приложения в самых разных областях, от финансов до физики, и все это было интересно представлено в видео Гриффина.

Нажмите здесь, чтобы посмотреть видео

В «Оригаметрии» Рин Фукуока использует оригами для построения правильных многоугольников, а также для разделения угла пополам. Судьи сочли видео очень свежим, игривым и минималистичным (ни слова не сказано, а написано лишь несколько). Уровень преподавания особенно искусный (например, обратите внимание на соответствующие паузы в рассуждении о трисекции после риторического вопроса «а почему?»). В этот момент и в других местах Рин демонстрирует большую чувствительность к аудитории.

Нажмите здесь, чтобы посмотреть видео

В своем проекте Мадлен использует музыкальный инструмент, известный как маримба, чтобы продемонстрировать нечто глубокое в музыке: музыкальная гармония тесно связана с отношениями небольших целых чисел, открытие, которое Пифагор и его последователи, как говорят, сделали 2500 лет назад. Судьи были впечатлены ясностью и элегантностью объяснений и демонстраций Мадлен.

Нажмите здесь, чтобы посмотреть видео Мэдлин.

У Джибрана есть сайт в Instagram, @creative_math, где он знакомит старшеклассников с темами, которые обычно предназначены для студентов-математиков. Судьи восхищались привлекательностью его постов и тем, как умело он объясняет передовые математические идеи, всегда дружелюбным голосом.

Нажмите здесь, чтобы прочитать сообщения Джибрана.

Алисса написала статью, в которой объясняет оптимальную стратегию игры в крестики-нолики, а также исследует варианты игры на сетке 4×4 и в кубической решетке 3x3x3 в трех измерениях. Судьи оценили ясность и оригинальность расследований Алисы.

Нажмите здесь, чтобы прочитать статью Алиссы.

Проект

Коула представлял собой эссе о «несоответствии между тем, как математика обычно изображается, и тем, как она выполняется на самом деле». Учебники и статьи по математике обычно стараются выглядеть безупречно, но любой, кто занимается математикой, знает, насколько грязным и запутанным может быть то, что вы делаете на самом деле. Коул взял интервью у нескольких математиков об этом разрыве и выдвинул убедительный аргумент, что математическое общение будет более эффективным, если мы очеловечим его, показывая наши ошибки, а также наши идеи.

Нажмите здесь, чтобы прочитать эссе Коула

Для своего проекта Ян сконструировал песню из цифр иррационального числа, известного как золотое сечение (также известное как божественная пропорция из-за его красоты). Все судьи сочли проект интригующим как исследование и сочли саму песню удивительно красивой.

Нажмите здесь, чтобы послушать песню Яна.

Мадлен создала портрет математика Валери Томас. Судьи были впечатлены изобретательностью этого проекта: в нем используются только символы «3D» — искусно расположенные — для создания сильно вызывающего воспоминания портрета математика, известного своей работой над трехмерными спутниковыми изображениями.

Хелена написала «найденное стихотворение» — стихотворение, в котором каждое слово (кроме «вы» и «нас») взято из другого источника, в данном случае из статьи Эрика Вайсштейна MathWorld «Фундаментальные теоремы исчисления». Хелена переставила слова так, чтобы получилось что-то совершенно неожиданное, сдержанное маленькое стихотворение, от которого у судей перехватило дыхание.

Нажмите здесь, чтобы прочитать стихотворение Хелены.

Шрея и Эми объединились, чтобы воплотить в жизнь комбинаторную идентичность. Используя баскетбол в качестве математической площадки, они продемонстрировали два подхода к вычислению того, сколькими способами игрок может сделать или промахнуться 9 раз. н . Видео глупое и веселое: Эми пишет (и игриво болтает), пока Шрея стреляет, и, прежде чем вы это узнаете, они вычислили тождество для суммы биномиальных коэффициентов. Судьям понравилась простая, но умная видеосъемка, подшучивания между девушками и их аккуратные объяснения математики.

Нажмите здесь, чтобы посмотреть видео

Заявка Джулии Шанан на соискание Строгацкой премии представляла собой стихотворение свободного стиха под названием «Человек-математик». Судьи были тронуты артистизмом и эмоциональной силой стихотворения, его глубиной и откровенной честностью, блестящим использованием языка и вниманием к неожиданным, но красноречивым деталям. «Математический человек» передает — одновременно красиво и навязчиво — изоляцию, которую Джулия чувствовала как одну из единственных девочек на Американском математическом конкурсе в 10-м классе, и, что более важно, интеллектуальную изоляцию, которую она все еще испытывает каждый день как человек, который все еще глубоко любит математику. не хватает друга, с которым можно было бы поделиться.

Мама предлагает зайти в Panera, чтобы получить удовольствие от всех болезненных математических вычислений, которые я только что пережил.

Вот только это было не больно.

Я из тех, кто просидел медленную математику в средней школе, скучая и мечтая,

не видя, для чего все это было, желая — но никогда не напрягая дух, чтобы добиться большего.

Пока нет.

Теперь я не хочу Panera.

Я не хочу, чтобы меня похлопывали по плечу и не понимали.

Я хочу вернуться в эту аудиторию, закончить экзамен и говорить об этом всю ночь.

Судьи сочли, что их собственных слов недостаточно, чтобы обобщить достижения Джулии в написании «Math Person». Скажем так, прочтите ее стихотворение и испытайте его на себе.

Нажмите здесь, чтобы прочитать стихи Джулии.

Апурва Панидапу — 16-летняя студентка-математик, художница и защитник интересов молодежи и гендерных меньшинств в STEAM. Она ведет блог под названием «Жемчужины STEM» и часто публикует эссе на Cantor’s Paradise, математическом сайте №1 на Medium.com. Она считает свой блог «местом, где можно узнать математические темы в доступной и беззаботной форме. Я предполагаю не более чем базовые математические знания и добавляю забавные факты для учащихся всех уровней опыта. Как для себя, так и для читателей, я вплетаю поп-культуру, пикапы и невероятные истории, чтобы познакомить людей с фантастическим миром математики и показать им, что любой может получать удовольствие от чего угодно».

Судьи были очень впечатлены радостными, элегантно написанными сообщениями в блоге Апурвы по широкому кругу математических тем, от парадокса лжеца и разбиений до тесселяций и фракталов. Сочетая четкие объяснения с привлекательным макетом и хорошо подобранной графикой, Gems in STEM сама по себе является жемчужиной. Жюри понравилось разнообразие постов в блоге Апурвы. Они затрагивают историю, этимологию и головоломки, а также устанавливают связь со всем, от искусства и архитектуры до науки и природы. Воодушевляющее послание Апурвы состоит в том, что математика есть везде и доступна любому человеку с любым образованием.

Нажмите здесь, чтобы прочитать сообщения Апурвы.

Анимационное видео

Ширли наполнено шутками и отсылками к поп-культуре, рассчитанными на более молодую аудиторию (хотя зрителям, состоящим из судей постарше, оно тоже очень понравилось). Ее цель, как она говорит в своем эссе, состоит в том, чтобы демистифицировать «математику с помощью юмора, забавных анимаций и реальных сценариев». В своем видео Ширли иллюстрирует технику комбинаторики, известную как «Палки и камни» (или «Звезды и бруски»), рассказывая историю о дилемме дедушки Боба: три его внучки. Благодаря отличной педагогике (в том числе попаданию в заманчивую математическую ловушку и последующему показу, как из нее выбраться) видео показывает зрителю, как посчитать все способы, которыми дедушка Боб может решить свою задачу. Видео веселое и динамичное, но уделяет нужное количество времени более сложным идеям и разбавляет их красочной графикой и выбором слов.

Нажмите здесь, чтобы посмотреть видео Ширли

Видео

Кэтрин было вдохновлено ее попытками понять, почему пустое множество является подмножеством каждого множества. Как она написала в своем эссе для этого конкурса: «Я никогда не принимала и не запоминала математическое понятие, если оно не имело для меня полного смысла, поэтому я решила выйти за рамки простых чисел и провести аналогию. Я понял, что наборы на моей странице могут быть связаны с моими занятиями в школе. Как элементами математического множества являются числа, так элементами класса являются ученики. Когда некоторые из них отсутствуют, существует только «подмножество» класса. И когда все отсутствуют, подмножество класса все еще существует, поскольку технически период класса все еще происходит. Эту аналогию я не хотел держать при себе, и поэтому она стала основой моего участия в конкурсе на Строгацкую премию!»

Судьи оценили доходчивые объяснения Кэтрин и сопровождающие их рисунки. Теорию множеств часто считают одной из самых абстрактных частей математики, но в руках Кэтрин она становится осязаемой и яркой. Ее аналогия с классной комнатой должна понравиться любому ученику. Кроме того, Кэтрин дает зрителю представление об универсальности теории множеств и о вкусе ее приложений в компьютерных науках.

Нажмите здесь, чтобы посмотреть видео Кэтрин

В этом видео об известной теореме из теории графов и топологии Смаян красиво объясняет, почему любую плоскую карту можно раскрасить всего четырьмя цветами, так что соседние страны всегда будут разными цветами. Видео нежное и ясное, оживленное обильной графикой, аккуратно синхронизированной с повествованием Смаяна. Он дает зрителю полезную интуицию о том, как можно использовать неравенства (для вершин, ребер и граней плоских графов), чтобы сократить, казалось бы, бесконечную проблему до конечного числа случаев, которые затем могут быть проверены компьютером. Судьи сочли, что это была очень четкая презентация глубокого результата по продвинутой математике, объясненная таким образом, что каждый может понять и получить удовольствие.

Нажмите здесь, чтобы посмотреть видео Смаяна

Джазовый саксофонист и математик Маркус Дж. Миллер поделится своими размышлениями о том, как математика и музыка могут сделать нас цельными.

Маркус Г. Миллер — музыкант и математик, живущий в Нью-Йорке.

Джон Уршель, нынешний кандидат математических наук в Массачусетском технологическом институте и бывший профессионал НФЛ, делится своей любимой логической головоломкой.

Джон Уршель играл в профессиональный футбол за «Балтимор Рэйвенс» с 2014 по 2017 год, прежде чем уйти на пенсию, чтобы сосредоточиться на своей карьере в области математики. В настоящее время он является кандидатом наук в Массачусетском технологическом институте, где изучает теорию спектральных графов, числовую линейную алгебру и машинное обучение.

Приготовьтесь принять участие в сумасшедшей и забавной головоломке Kahoot со Стивом Шерманом. Это викторина, которая пощекочет ваши мозговые струны и бросит вызов вашим мыслительным способностям. Некоторые головоломки будут легкими, а другие заставят вас задуматься. Есть ли у вас что требуется, чтобы стать нашим чемпионом по головоломкам?

Необходимые материалы:

Смартфон, планшет или персональный компьютер с доступом в Интернет

Стив Шерман — директор по воображению и исполнительный мечтатель компании Living Maths.

Во время посещения MoMath покойный великий Джон Хортон Конвей произвел впечатление на людей, мгновенно указав им день недели, на который приходится или будет приходиться та или иная дата. И вы тоже можете это сделать! На какое число недели в следующем году выпадет твой день рождения? Или твой юбилей? Или любимый праздник? Когда следующая пятница 13-е? В какой день недели вы родились? Настройтесь на презентацию мастера головоломок MoMath Питера Винклера о чудесном «правиле Судного дня». Это легко и весело, и немного потренировавшись, вы сможете повторить подвиг Конвея. Это отличный трюк, и он продуман так, чтобы вы могли запомнить его и использовать, когда это необходимо.

Необходимые материалы:

Бумага
Карандаш

Питер Винклер в настоящее время является заслуженным председателем MoMath по общественному распространению математики и профессором математики и компьютерных наук в Дартмутском колледже.

Присоединяйтесь к Карлу Шафферу, пока мы играем с несколькими удивительными способами движения конечностями по кругу. Применяйте эти действия для создания последовательностей движений с идеальной математической опорой — обычным листом бумаги. Затем узнайте, как это связано с любопытной алгеброй кватернионов!

Необходимые материалы:

Несколько листов бумаги для принтера размером 8,5″ на 11″
Зона размером 5 на 5 футов для перемещения (предпочтительна зона без коврового покрытия)

Карл Шаффер () — танцор, хореограф, математик и профессор математики в колледже Де Анза.

Какое отношение текучесть топологии и узлов может иметь к жесткости операций над дробями? Присоединяйтесь к Алексу Конторовичу, чтобы узнать об увлекательной связи, открытой покойным математиком Джоном Конвеем.

Необходимые материалы:

2 шнура разных цветов (можно также использовать провода или шнурки)
Поверхность для укладки струн (например, пол или стол)
Дополнительные материалы: бумага и карандаш

Алекс Конторович — декан академического содержания MoMath и профессор математики в Rutgers.

Эксперт по оригами Венди Зейхнер научит делать одну или две модели оригами, которые можно сложить из обычной бумаги для принтера. В каждой строчке есть математика!

Необходимые материалы:

Несколько листов бумаги для принтера 8,5 x 11 дюймов
Ручка или карандаш
Ножницы

Венди Зейхнер — эксперт по оригами и президент OrigamiUSA.

Превратите два листа плотной бумаги и немного скотча в волчок и исследуйте его геометрию! Присоединяйтесь к Яне Моханти, доктору философии, математику и изобретателю Geometiles®, которая проведет вас через это увлекательное занятие по STEM. Вам будет предоставлен шаблон для печати и показано, как превратить его в свой спиннер. Как только вы освоите простую конструкцию, вы сможете украсить свой спиннер собственным дизайном.

Необходимые материалы (метрические эквиваленты указаны в скобках) :

2 листа картонной бумаги размером 8,5 x 11 дюймов (размер A4), желательно двух цветов; Папки manila, обрезанные до размеров 8,5 x 11 дюймов, также подойдут
Ножницы
Лента
Дополнительно: этот проект также можно собрать из мини-набора Geometiles® 2, который можно приобрести в Additions , интернет-магазине MoMath.

Яна Моханти — преподаватель математики, математик и создатель Geometiles®.

Если бы повторные подбрасывания монеты определяли, какой шаг вы предпримете, вы бы куда-нибудь попали? Шагните прямо (принесите свою монету) и узнайте!

Необходимые материалы:

1 монета
Бумага
Карандаш

Ральф Пантоцци — лауреат Премии Розенталя 2014 года и лауреат Президентской премии в области преподавания математики.

Давайте откроем для себя магию многогранной формулы Эйлера, создавая структуры из зубочисток и зефира.

Необходимые материалы:

1 коробка традиционных закругленных зубочисток с остриями на обоих концах
1 пакет мини-зефира
Бумага
Карандаш

Брюс Бэйли () — профессор математики в Аризонском университете и водитель автобуса, участвовавший в роуд-шоу Arizona Mathematics Road Show.

Присоединяйтесь к нам в онлайн-приключении по математике и бумаге! Годвин Моррис, директор образовательного центра Dazzling Discoveries STEM, продемонстрирует некоторые задачи по инженерному делу с бумагой. Вместе мы изучим пропорции, пропорции и масштабы, пока Годвин покажет вам, как создавать строения, мебель и персонажей из простых материалов.

Необходимые материалы:

Бумага для принтера
Лента
Ножницы

Годвин Моррис — директор Образовательного центра Dazzling Discoveries STEM.

Доктор Артур Бенджамин поразит вас математической магией, а затем научит вас, как это делать. Принеси калькулятор!

Необходимые материалы:

Калькулятор

Арт Бенджамин — отмеченный наградами популярный артист, математик и профессор математики в колледже Харви Мадда.

Возьмите с собой что-нибудь гибкое — галстук, шнурок, кусок веревки — и давайте повеселимся, изучая любопытную математику складывания.

Необходимые материалы:

Что-нибудь гибкое, например, галстук, шнурок или веревка

Джеймс Тэнтон — всемирно известный педагог, популяризатор математики и математик.

Педагог и артист Джон Чейз покажет вам тесную связь между математикой и жонглированием. Математическое моделирование дало жонглерам множество новых моделей для жонглирования, и мы приглашаем вас посмотреть, на что способна математика. Принесите три предмета для жонглирования, чтобы присоединиться к веселью!

Необходимые материалы:

3 предмета для жонглирования

Джон Чейз — математический жонглер и преподаватель математики.

Манджул Бхаргава продемонстрирует интерактивный фокус, демонстрирующий, как можно создать удивительную сложность из чрезвычайной простоты. Зрителям предлагается участвовать из дома!

Необходимые материалы:

4 игральные карты

Манджул Бхаргава г. — первый заслуженный приглашенный профессор MoMath за общественное распространение математики, профессор математики в Принстонском университете и призер Филдса.

Приходите и насладитесь внеконкурсными исследованиями по математике.

Марк Сол — старший научный сотрудник Математического фестиваля Джулии Робинсон.

Синди Лоуренс, исполнительный директор MoMath, и Тим Ниссен, заместитель директора MoMath, приветствуют всех на пятом ежегодном нью-йоркском математическом фестивале, который включает часы математического веселья и развлечений. Присоединяйтесь к докладчикам со всего мира, чтобы разделить день оживленных и увлекательных мероприятий.

Джеймс Тэнтон, председатель Консультативного совета MoMath, открывает фестиваль, поделившись весьма интригующим «Международным математическим приветствием». Вы можете понять, как это работает?

Сайт фестиваля открывается в 13:30 по восточному поясному времени (Нью-Йорк). Войдите в любое время с 13:30 до 14:00, чтобы просмотреть любимую картинку MoMath прошлых лет. Мероприятия начинаются ровно в 14:00 по восточному поясному времени (Нью-Йорк).

Ознакомьтесь с нашей подборкой Geometiles® и найдите книги ведущих фестиваля Питера Винклера и Арта Бенджамина.

Специалист отдела розничной торговли MoMath всегда готов ответить на вопросы и дать квалифицированный совет по выбору всех ваших математических подарков.

Зайдите, чтобы посмотреть подборку кубиков Рубика, просмотреть восхитительные книги Кристофера Дэниелсона, Какой из них не принадлежит? и Сколько? , и узнайте больше о фильме Человек, который познал бесконечность , в котором Манджул Бхаргава работал техническим консультантом, чтобы обеспечить точность математических расчетов, показанных в фильме.

Специалист по розничной торговле MoMath всегда готов ответить на вопросы и дать квалифицированный совет по выбору всех ваших математических подарков.

Ознакомьтесь с подборкой цветной бумаги для оригами MoMath, книгой Карла Шаффера Math Dance и другими замечательными предметами из Additions, интернет-магазина MoMath.

Специалист MoMath по розничной торговле всегда готов ответить на вопросы и дать квалифицированный совет по выбору всех ваших математических подарков.

Посмотрите, как Лорен Роуз собирает мозаику из кубика Рубика, и попытайтесь угадать, какой получится картинка. Математика встречается с искусством в этом творческом приложении популярного кубика Рубика.

Лорен Роуз — математик и профессор математики в Бард-колледже.

Даниэль Роуз-Левин продемонстрирует, как он собирает кубик Рубика ногами менее чем за 20 секунд.

Дэниел Роуз-Левин — бывший рекордсмен мира по сборке кубика Рубика с ногами.

Как невидимый мир пантомимы может исследовать математические идеи? Присоединяйтесь к Тиму Шартье, поскольку он использует пантомиму для исследования веса, величины силы и проективного движения с помощью искусства пантомимы. Вы также узнаете, как сделать бесконечную плитку шоколада. (Шоколадный батончик является настоящей опорой, но еда изображается пантомимой, поэтому удовольствие не содержит калорий.)

Тим Шартье — математический мим и профессор математики в колледже Дэвидсона. Он выступал по всему миру и прошел обучение в нескольких школах пантомимы, в том числе на мастер-классах у легендарного Марселя Марсо.

Симметрия вокруг нас. Мы видим симметрию в наших телах, автомобильных колесах, заборах, тканевых узорах, логотипе MoMath и многих других объектах! Мы узнаем о различных типах симметрии и весело проведем время, создавая симметричное искусство, используя обычные объекты.

Дэвид Рейманн — профессор математики и информатики колледжа Альбион, а также художник, который использует симметрию в своих работах.

Является ли лифт транспортным средством? Хот-дог — это бутерброд? Является ли сердце формой? Смайлик — это слово? Ответы на эти вопросы зависят от ваших определений транспортного средства, бутерброда, формы и слова. Точные определения являются важными инструментами математики, но немногие определения начинаются с такой точности, какой они потребуются позже. Поиграйте с границей между точностью и двусмысленностью в этой динамичной совместной сессии.

Кристофер Дэниэлсон () — отмеченный наградами писатель и преподаватель математики.

Присоединяйтесь к мистеру А., когда он поделится одним из своих многочисленных математических рэпов, расскажет, как он начал читать рэп о математике, и познакомит вас с некоторыми математическими идеями и ссылками в рэпе.

Майк Андрейковикс — учитель математики в старшей школе из Лонг-Айленда, штат Нью-Йорк, который создает и исполняет рэп о математике на основе популярных треков хип-хопа.

Кристофер Дэниелсон — отмеченный наградами писатель и преподаватель математики.

Синди Лоуренс — исполнительный директор и генеральный директор Национального музея математики.

Тим Ниссен — заместитель директора Национального музея математики.

Стив Шерман — главный специалист по воображению и исполнительный мечтатель компании Living Maths.

Питер Винклер — почетный приглашенный профессор MoMath, занимающийся общественным распространением математики.

Карл Шаффер — танцор, хореограф, математик и профессор математики в колледже Де Анза.

Алекс Конторович — декан академического содержания MoMath и профессор математики в Rutgers.

Арт Бенджамин — отмеченный наградами популярный артист, математик и профессор математики в колледже Харви Мадда.

Брюс Бэйли — певец, скрипач и профессор математики Аризонского университета.

Дэниел Роуз-Левин — бывший рекордсмен мира по сборке кубика Рубика с ногами.

Дэвид Рейманн — профессор математики и информатики колледжа Альбион, а также художник, который использует симметрию в своих работах.

Годвин Моррис — директор образовательного центра Dazzling Discoveries STEM.

Джеймс Тантон — всемирно известный педагог, популяризатор математики и математик-исследователь.

Джон Чейз — математический жонглер и преподаватель математики.

Лорен Роуз — танцовщица, хореограф, математик и профессор математики в колледже Де Анза.

Манджул Бхаргава — почетный приглашенный профессор MoMath за общественное распространение математики, профессор математики Принстонского университета и обладатель медали Филдса.

Марк Сол — исполнительный директор Математического фестиваля Джулии Робинсон.

Майк Андрейкович — учитель математики в средней школе из Лонг-Айленда, штат Нью-Йорк, который сочиняет и исполняет рэп о математике на основе популярных хип-хоп треков.

Эксперт по оригами Венди Зейхнер — исполнительный директор Origami USA.

Ральф Пантоцци — лауреат премии Розенталя 2014 года и преподаватель математики.

Яна Моханти — преподаватель математики, математик и создатель Geometiles®.

Кэролин Фигуэро — менеджер по розничной торговле Национального музея математики.

Тим Шартье — математический мим, профессор математики в колледже Дэвидсона.

Детали ТК

Livingston, NJ

«Цель Math Musings, журнала, который я начал в старшей школе, — писал Рохан Джа, — заключалась в том, чтобы показать, что математика повсюду, но часто мы не осознаем этого. Это лежит в основе музыки, которую мы играем, или в том, как природа использует ее для своей собственной оптимальной выгоды, или это может быть в причудливом карточном фокусе, или математика может помочь нам уменьшить повсеместно наблюдаемое раздражение от пробок в часы пик». Журнал разными способами пытается очеловечить и оживить математику: рассказывая анекдоты об известных математиках; бросая вызов однокурсникам с веселыми головоломками; или подтолкнув их к более глубоким идеям, таким как головоломка с кувшинками, которая приводит к понятию обратной рекурсии в финансах. С помощью четких иллюстраций и пошаговых инструкций по фокусам и другим действиям Рохан пытается сделать математику увлекательной для всех… и у нее это прекрасно получается.

Coronado, CA

Проект, представленный Kyna Airriess, представляет собой журнал, основанный на цитате из A Mathematician’s Lament , полемического эссе учителя средней школы Пола Локхарта. «Нет ничего более мечтательного и поэтичного, столь радикального, подрывного и психоделического, как математика», — писал Локхарт. Чтение эссе Локхарта, по словам Кины, «поспособствовало моему собственному превращению из ярого ненавистника математики в честолюбивого математика; Я никогда не слышал, чтобы кто-то описывал математику, предмет бесчувственных вычислений, такими словами, как «поэтический» и «радикальный». Прошло много времени, прежде чем я начал замечать эти черты для себя, но сегодня я идентифицирую себя как математика. ботаник, и я хочу изучать математику в колледже».

В журнале каждое из запоминающихся прилагательных Локхарта — мечтательный, поэтический, подрывной и психоделический — проиллюстрировано и связано с математическими идеями с использованием символов, истории, цвета и образов. Судьи были впечатлены страстной энергией, переданной словами и дизайном журнала. Общий эффект достигает того, что задумала Кина: воплотить «то, что те из нас, кто любит математику, хотят, чтобы мир понял. Дело вовсе не в холодных расчетах — это поле, полное творчества и красоты, и оно так же пропитано человечностью, как и любое другое».

Нью-Йорк, штат Нью-Йорк

«Лимерики и поэзия — нетипичный способ передать информацию о математике, — признает Сара Тау, — но я думаю, что это делает их более привлекательными, чем заучивание функций наизусть. Кто не любит лимерик?» Поэтому Сара создала серию коротких рифмованных стихотворений, чтобы перечислить некоторые основные свойства линейных, квадратичных, тригонометрических, полиномиальных, рациональных и других типов функций, встречающихся в алгебре и предварительном исчислении, и проиллюстрировала страницы примерами.

Судей поразила игривость этой работы. Лимерики — это беззаботная форма поэзии, в которой творчество исходит из работы в рамках ограничений и восхитительного их преодоления — и почти то же самое можно сказать о математике! В самом деле, как писала Сара: «Я люблю математику и всегда пытаюсь решать задачи, но это был новый тип задач. Тот, который не нуждался ни в алгебре, ни в моделировании. Каждое стихотворение становилось проблемой, которую нужно было решить, поскольку я пытался подобрать слова, чтобы свойства каждого функционального типа аккуратно рифмовались». Стихи освещают отличительные свойства различных видов функций и привлекают читателей уникальным, творческим и запоминающимся способом передачи математических идей.

Honolulu, HI

Проект Джона Йошиды представляет собой карандашно-бумажную инфографику по теории графов. Он говорит: «Я задумал эту идею, когда читал о том, как Артур Кейли использовал деревья для представления структур углеводородов с n атомами углерода и 2n+2 атомами водорода. Вся структура имитирует один из этих углеводородов, этан (n=2), и внутри каждого атома заключено уникальное применение теории графов. Я разделил страницу на две части, чтобы атомы водорода, связанные с левым углеродом, содержали головоломки и забавные приложения теории графов, а те, которые связаны с правым водородом, больше касались непосредственных приложений, очень похожих на левое и правое полушария нашего мозга». Например, Теорема о четырех цветах (забавное приложение теории графов к раскрашиванию карт и давний исследовательский вопрос) появляется слева, а правая сторона включает приложения графов к информатике (нейронные сети и остовные деревья) и электротехнике ( принципиальные схемы).

Судьи высоко оценили оригинальную концепцию дизайна этого графического изображения, которое подчеркивает универсальность и междисциплинарный дух теории графов. Слова и изображения сочетают в себе историю, математику, химию и психологию, а вопросы в небольших текстовых полях приглашают читателя провести собственное исследование.

Toronto, ON

«Мой математический коммуникационный проект, Infinity Universe , — пишет Ивонн Хонг, — представляет собой иллюстративное, но математическое описание мира, в котором мы живем. Каждый показанный неодушевленный объект представляет простую, но вездесущую концепцию математики: при ближайшем рассмотрении монохроматическое дерево — это фрактальное дерево Пифагора, галактика на заднем плане построена с использованием последовательности Фибоначчи, а планета и комета — это разные вариации дерева Пифагора. Аполлоновская прокладка. Infinity Universe продвигает универсальность математической коммуникации через абстракцию объектов и явлений, с которыми знакомы люди во всем мире».

Тщательно выполненная с большим вниманием к деталям картина, представленная Ивонн, привлекла судей своими яркими цветами и гипнотическими узорами. Более того, тема бесконечности пронизывает картину, как и всю математику. Но здесь предположение о бесконечности скорее волшебное и потустороннее, чем научное и буквальное, и поэтому может понравиться аудитории, обычно не привлекающей математику.

New York, NY

Зои Маркман создала наглядное доказательство «формулы суммы квадратов», искусно используя три деревянные трехмерные пирамиды, которые соединяются друг с другом. Каждая пирамида состояла всего из 1 ² + 2 ² + … + n ² одинаковых деревянных кубиков; таким образом, его объем визуально представлял собой сумму квадратов всех целых чисел от 1 до n. Чтобы найти формулу для этой суммы квадратов, Зои манипулировала и переставила три пирамиды, чтобы сформировать прямоугольную призму, объем которой затем можно было легко вычислить, чтобы получить желаемую формулу суммы квадратов.

Судьи согласились с Зои в том, что такого рода визуальные, практические манипуляции «обеспечивают более глубокое понимание математики, чем то, которое дает письменный проект. Поскольку вы можете наблюдать, держать и манипулировать пирамидами (даже лично), аудитория способна понять, почему формула работает, а не просто принимать ее за чистую монету и произвольно принимать ее за истину. Во-вторых, презентацию могли понять даже люди, не обладающие значительными математическими знаниями. Он изложил то, что выглядит пугающей проблемой, в легко усваиваемой форме». Зои даже проверила презентацию на друзьях, которые сказали, что им не нравится математика. Это хорошая практика в любой форме общения. В целом, этот проект скромный, но очень хорошо сделанный и производит очень приятное «Ага!» момент для многих зрителей; действительно, это заставило одного из судей понять «формулу суммы квадратов» совершенно по-новому!

Santa Monica, CA

Чтобы выразить универсальность математики, Катарина Ченг перевела ее на другой универсальный язык: танец. «Точно так же, как танец существует как часть многих культур по всему миру для выражения абстрактных идей и эмоций через движение, математика бросает вызов культурным линиям, чтобы выражать абстрактные идеи через структуры и формы на странице», — написала она в описании своего проекта. Ее видео «Dancing the Dihedral Group» стремилось с помощью танца «представить визуальные симметрии, в первую очередь квадратные», а с помощью слов «то, как они перевели в алгебру, в первую очередь группу D8».

Судьи хвалят Катарину за элегантность ее общения в видео. Особенно примечательной была эстетика минимализма — в том, как снимается видео, в выборе одежды, фона и цветов — все это идеально сочетается с минималистичной эстетикой теории групп. Интеграция математической графики с танцевальными движениями также выполнена изящно. Хотя другие в прошлом признавали сходство между математикой и танцем, немногие передавали эту аналогию с таким изяществом исполнения. Танцы и музыка тоже были искусно минимальными. Общий эффект заключается в усилении центральной идеи красоты в простоте.

Centreville, VA

Хамза Алсамраи любит Instagram, а также любит математику. Но когда он заметил, что в Instagram существует очень мало математических страниц, он попытался изменить это, запустив @daily_math, страницу, посвященную интригующим проблемам и идеям об алгебре, геометрии, исчислении, теории чисел и других разделах математики. «С помощью высококачественных образовательных постов, — говорит он, — я надеялся создать сообщество в Instagram, основанное на общей страсти к математике».

Судьи были впечатлены творчеством Хамзы, выраженным в умелом использовании визуальных эффектов, истории и головоломок, представленных в привлекательной форме. Его объяснения математических понятий ясны и проницательны, и он очень интерактивен со своими подписчиками, даже приглашая их публиковать сообщения. Судьи также высоко оценивают его рост как создателя и коммуникатора. Его страница в Instagram превратилась из сосредоточения внимания на сложных интегралах в первые дни на решение более доступных задач сейчас, и визуальное представление развивалось в тандеме. Благодаря своему привлекательному выбору дизайна, который способствует четкому общению, он все более эффективно использует сильные стороны среды Instagram.

Сентервилль, Вирджиния

Нажмите здесь, чтобы открыть аккаунт Daily Math в Instagram.

Нажмите здесь, чтобы открыть учетную запись Daily Math Tik Tok.

Количество комбинаций – Зона Рубика

Сколько комбинаций у кубика Рубика? Узнать, сколько у 3x3x3, несложно, но когда я просмотрел, оказалось, что драгоценных страниц, показывающих количество комбинаций для всех размеров от 2x2x2 до 7x7x7, было очень мало. Итак, я сделал эту страницу, перечислив количество комбинаций для кубиков разного размера. Также есть калькулятор javascript на случай, если вы захотите рассчитать его для больших размеров.

Кубик Рубика 2x2x2 (называемый Pocket Cube ) имеет 3674160 комбинаций . Это управляемый номер. Если вы возитесь с кубом 2x2x2 случайным образом, восемь часов в день непрерывно, вы будете собирать его по чистой случайности примерно два или три раза в год. Предполагая, что ваш кубик — или ваше запястье — не сломается за это время. Имейте в виду, четыре месяца на сборку кубика 2×2 несколько медленнее, чем мировой рекорд.
Оригинальный кубик Рубика 3x3x3 имеет 43 252 003 274 489 856 000 комбинаций , или 43 квинтиллиона. Опять же, как указано на главной странице этого веб-сайта, это управляемое число. Например, это немного меньше, чем квадрат населения Земли.
Кубик Рубика 4x4x4 (называемый Master Cube или Rubik’s Revenge — не знаю, за кого он мстил, должен сказать) имеет 7 401 196 841 564 901 869 874 093 974 498 574 336 000 001 комбинаций (6 7,4 quattuordecillion, если вы действительно хотите знать). Чтобы понять, насколько велико это число, представьте, что у вас есть столько же чайных ложек сахара (скажем, вы планируете очень большое чаепитие ). Сахар заполнил бы Солнечную систему примерно в 3,5 раза больше орбиты Плутона. Он также будет весить примерно в 70 раз больше, чем наша галактика, и мгновенно рухнет в черную дыру со взрывом, который сотрет Млечный Путь, Магеллановы облака и, вероятно, разбудит некоторых сонных андромедианцев. Подумайте об этом в следующий раз, когда будете крутить 4×4.
Как будто этого недостаточно, 5x5x5 кубик Рубика (называемый Профессорским кубиком) имеет 282 870 942 277 741 856 536 180 333 107 150 328 293 127 731 985 672 134 721 536 000 000 000 000 000 комбинаций (он же 283 trevigintillion). Это становится неприятно близким к количеству атомов в известной Вселенной.
Недавно греческий инженер Панайотис Вердес придумал, как делать кубики 6×6 и 7×7. The V-Cube 6 (a 6x6x6 Rubik’s cube) has 157 152 858 401 024 063 281 013 959 519 483 771 508 510 790 313 968 742 344 694 684 829 502 629 887 168 573 442 107 637 760 000 000 000 000 000 000 000 000 комбинаций . Это, конечно, смехотворно огромное число, но…

.
The 7x7x7 Rubik’s cube (the V-Cube 7 ) has 19 500 551 183 731 307 835 329 126 754 019 748 794 904 992 692 043 434 567 152 132 912 323 232 706 135 469 180 065 278 712 755 853 360 682 328 551 719 137 311 299 993 600 000 000 000 000 000 000 000 000 000 000 000 комбинации. Как я указываю в этом фильме, это больше комбинаций, чем восемь независимых кубиков 3x3x3. И все же некоторые люди все еще могут решить 7x7x7 всего за несколько минут. Удивительно!

Никто еще не строил и не продавал кубы большего размера, хотя Панайотис Вердес обещает, что в разработке находятся и более крупные кубы. Между тем, существуют программы, которые позволят вам играть с кубом любого размера. Эти большие размеры решать не сложнее, чем 6×6 и 7×7, просто более утомительно.

An 8x8x8 cube would have 35 173 780 923 109 452 777 509 592 367 006 557 398 539 936 328 978 098 352 427 605 879 843 998 663 990 903 628 634 874 024 098 344 287 402 504 043 608 416 113 016 679 717 941 937 308 041 012 307 368 528 117 622 006 727 311 360 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000.
A 9x9x9 cube would have 14 170 392 390 542 612 915 246 393 916 889 970 752 732 946 384 514 830 589 276 833 655 387 444 667 609 821 068 034 079 045 039 617 216 635 075 219 765 012 566 330 942 990 302 517 903 971 787 699 783 519 265 329 288 048 603 083 134 861 573 075 573 092 224 082 416 866 010 882 486 829056 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 комбинации.
a 10x10x10 Cube будет иметь 82 983 598 512 782 362 708 769 381 780 036 344 745 129 162 094 677 382 883 567 691 311 764 021 348 095 163 778 367 367 211 211 764 0211 348 095 163 77 77 367 211 211 764 0211 348 095 163 77 77 247 21111117 887 88 387 88 367 211 211 211 764 098 163 78 78 78 383 367 211 211 211 764 098 1677 78 78 383 78 367. 902 768 732 457 008 486 832 096 777 758 106 509 177 169 197 894 747 758 859 723 340 177 608 764 906 985 646 389 382 047 319 811 227 549 112 086 753 524 742 719 830 99комбинация Ты!

Если вы хотите узнать количество комбинаций для куба большего размера, вы можете сделать это, используя форму ниже. Должен предупредить вас, что если вы наберете нелепый размер куба (скажем, более 30), он затормозит ваш компьютер, а не мой.

Примечание. Из-за ошибок в Internet Explorer вам может потребоваться использовать Google Chrome или Mozilla Firefox, чтобы исправить эту форму, пока я не найду способ обойти эти ошибки.

РубрикаРазное