Уклон 1 2: Обозначение уклона на чертежах

Содержание

Конусообразные конструкции. Как начертить уклоны и конусность

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон . Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона . На примере (рисунок) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах . Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307-68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность . Конусностью называется отношение диаметра основания конуса к высоте. Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах . Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с. Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.
Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

Во многих деталях машин используются уклоны и конусность. Уклоны встречаются в профилях прокатной стали, в крановых рельсах, в косых шайбах и т. д. Конусности встречаются в центрах бабок токарных и других станков, на концах валов и ряда других деталей.

Уклон характеризует отклонение прямой линии от горизонтального или вертикального направлений. Для того чтобы построить уклон 1:1, на сторонах прямого угла откладывают произвольные, но равные величины (рис. 1). Очевидно, что уклон 1:1 соответствует углу в 45 градусов. Чтобы построить линию с уклоном 1:2, по горизонтали откладывают две единицы, для уклона 1:3 — три единицы и т. д. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е.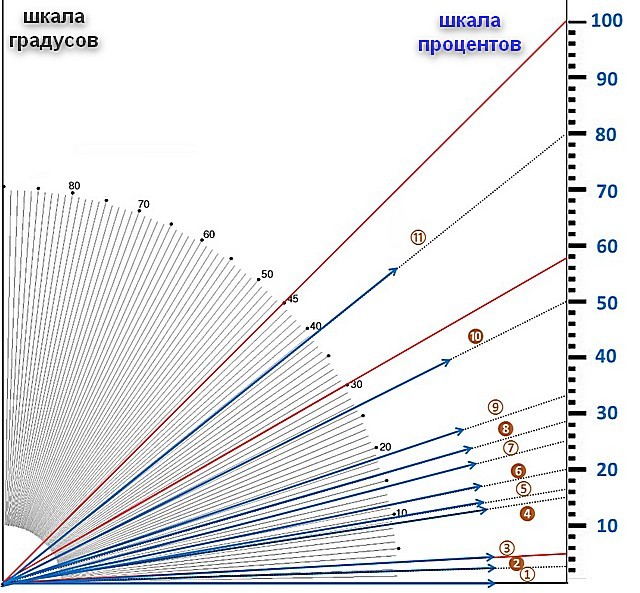 он выражается тангенсом угла а. Величину уклона на чертеже в соответствии с ГОСТ 2.307-68 указывают с помощью линии-выноски, на полке которой наносят знак уклона и его величину. Расположение знака уклона должно соответствовать определяемой линии: одна из прямых знака должна быть горизонтальна, другая — наклонена примерно под углом 30° в ту же сторону, как и сама линия уклона.

На рисунке в качестве примера построен профиль несимметричного двутавра, правая полка которого имеет уклон 1:16. Для ее построения находят точку А с помощью заданных размеров 26 и 10. В стороне строят линию с уклоном 1:16, для чего по вертикали откладывают, например, 5 мм, а по горизонтали 80 мм; проводят гипотенузу, направление которой определяет искомый уклон. С помощью рейсшины и угольника через точку А проводят линию уклона, параллельную гипотенузе.

Конусностью называют отношение диаметра основания к его высоте. В этом случае конусность К=d/l. Для усеченного конуса К = (d-d 1)/l . Пусть требуется построить конический конец вала по заданным размерам: d — диаметр вала — 25 мм;

I — общая длина конца вала — 60 мм; l 1 — длина конической части — 42 мм; d 1 — наружный диаметр резьбы — 16 мм; К — конусность 1: 10 (рис.

3, б). Прежде всего, пользуясь осевой, строят цилиндрическую часть вала, имеющую диаметр 25 мм. Этот размер определяет также большее основание конической части. После этого строят конусность 1:10. Для этого строят конус с основанием, равным 10 мм, и высотой, равной 100 мм (можно было бы воспользоваться и размером 25 мм, но в этом случае высота конуса должна быть взята равной 250 мм, что не совсем удобно). Параллельно линиям найденной конусности проводят образующие конической части вала и ограничивают ее длину размером 42 мм. Как видно, размер меньшего основания конуса получается в результате построения. Этот размер обычно не наносят на чертеж. Запись М16X1,5 является условным обозначением метрической резьбы, о чем подробнее будет сказано дальше.

TBegin—>

TEnd—>

Рис. 1. Построение уклонов

Перед размерным числом, характеризующим конусность, наносят условный знак в виде равнобедренного треугольника, вершину которого направляют в сторону вершины самого конуса. Знак конусности располагают параллельно оси конуса над осью или на полке линии-выноски, заканчивающейся стрелкой, как в случае надписи уклона. Конусность выбирают в соответствии с ГОСТ 8593-57 .

Рис. 2. Пример построения уклонов

TBegin—>

TEnd—>

Рис. 3. Построение конусности

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры начертательной геометрии и черчения

21 июня 2011г.

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ –

УКЛОНЫ, КОНУСНОСТЬ, СОПРЯЖЕНИЯ

Методические указания для всех специальностей

Квалификация выпуска «Бакалавр»

Ростов-на-Дону

Геометрические построения – уклоны, конусность, сопряжения:

Методические указания для всех специальностей. — Ростов н/Д: Рост. гос.

строит. ун-т, 2011. – 8с.

Составитель: ассист. А.В. Федорова

Редактор Н.Е. Гладких Темплан 2011 г., поз. 137.

Подписано в печать 6.07.11. Формат 60х84/16.

Бумага писчая. Ризограф. Уч.-изд.л. 0,3. Тираж 20 экз. Заказ 341.

____________________________________________________________________

Редакционно – издательский центр Ростовского государственного строительного университета.

344022, Ростов – на – Дону, ул. Социалистическая, 162

Ростовский государственный строительный университет, 2011

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ – УКЛОНЫ, КОНУСНОСТЬ,

СОПРЯЖЕНИЯ

При изготовлении профилей прокатной стали, боковые полки выполняют так, что плоскости, ограничивающие их, не параллельны, а расположены под некоторым углом между собой.

В технике часто применяются конические детали. При вычерчивании чертежей многих деталей приходится выполнять ряд геометрических построений, и в этой связи рассмотрим следующие понятия: уклоны, конусность, сопряжения.

Уклон – наклон одной прямой линии к другой (рис. 1).

Уклон i прямой АС определяется из прямоугольного треугольника АВС как отношение противолежащего катета ВС к прилежащему катету АС (рис.2):

Уклон может быть выражен в процентах (например, уклон в 10%

внутренних граней полок швеллера по ГОСТ 8240-89, рис. 3), отношением двух чисел (например, уклоны 1:20 и 1:4 граней рельса по ГОСТ 8168-75*) или в промилях (например, уклон 5‰ арматуры).

Знак уклона “ “, вершина которого должна быть направлена в сторону уклона, наносят перед размерным числом, располагаемым непосредственно у изображения поверхности уклона, или на полке линии – выноски, как показано на рисунках.

Построение уклонов

1. Провести прямую с уклоном i = 1:6 относительно прямой АЕ через точку А, лежащую на прямой АЕ (рис.3).

А 1 2 3 4 5 6С Е

Отложим на прямой АЕ от точки А шесть произвольно выбранных единиц. Через полученную точку В восстановим перпендикуляр к АЕ длиной в одну единицу.

Гипотенуза АС построенного прямоугольного треугольника АВС

является искомой прямой с уклоном 1:6.

Построение полок швеллера и двутавра

На рис. 4 и 5 показано построение уклона внутренней грани верхней полки швеллера и двутавра. Построен вспомогательный треугольник ВСD с

катетами 10 и 100мм для швеллера и 12 и 100мм для двутавра.

На горизонтальном отрезке «b» отложим отрезок, равный (b-d)/2 – для швеллера и (b-d)/4 – для двутавра. Из полученной точки проведем перпендикуляр длиной t. Отложенные размеры определили положение точки К,

через которую проходит прямая с уклоном 10% для швеллера и 12% — для двутавра. Через точку К провести прямую, параллельную гипотенузе построенного треугольника.

КОНУСНОСТЬ

Конусностью называется отношение диаметра окружности основания D

прямого конуса к его высоте h (рис.6).

К D h.

Для усеченного кругового конуса – отношение разности диаметров двух нормальных сечений конуса к расстоянию между ними (рис.7), т.е.

Конусность, как и уклон, может быть выражена отношением целых чисел или в процентах.

Перед размерным числом, характеризующим конусность,

наносят знак “ ”, острый угол которого должен быть направлен в сторону вершины конуса.

При одном и том же угле конусность в два раза больше уклона, так как уклон образующей конуса равен отношению радиуса его основания к высоте, а

конусность – отношению диаметра к высоте.

Таким образом, построение конусности i: n относительно данной оси сводится к построению уклонов i: 2n с каждой стороны оси.

СОПРЯЖЕНИЯ

Сопряжением называется плавный переход по кривой от одной линии,

прямой или кривой, к другой.

Построение сопряжений основано на свойствах прямых, касательных к окружностям, или на свойствах касающихся между собой окружностей.

Построение касательной к окружности

При построении прямой, касательной к

А окружности в заданной точке С, проводят прямую перпендикулярно к радиусу ОС. При

нахождении центра окружности, касающейся заданной прямой в точке С, проводят через эту точку перпендикуляр к прямой и откладывают на нем величину радиуса заданной окружности (рис. 8).

Построение внешней касательной к двум окружностям

Из центра О1 проводят вспомогательную окружность радиусом R3 = R1 -R2

и находят точку К. Построение точки К аналогично построению точки С. Точку О1 соединяют с точкой К прямой и проводят параллельную ей прямую из точки О2 до пересечения с окружностью. Точки сопряжения С1 и С2 лежат на пересечении прямых О1 К и ранее проведенной линии из центра О2 с

окружностями радиусов R1 и R2 (рис. 9).

А С 1

O 1

С 2В

R 2

Сопряжение двух дуг окружностей

При внешнем касании двух окружностей расстояние между центрами О1

и О2 равно сумме радиусов R1 и R2 . Точка касания С лежит на прямой,

соединяющей центры окружностей (рис.10).

При внутреннем касании окружностей О1 О2 = R1 — R2 . Точка касания С лежит на продолжении прямой О1 О2 (рис.11).

O1 СO2

R1 +R2

Рис.10 Рис.11

Сопряжение двух дуг окружностей дугой заданного радиуса

Из центров О1 и О2 описываются дуги вспомогательной окружности радиусом R3 = R + R1 и R4 = R + R2 (при внешнем сопряжении, рис. 12)

или R3 = R — R1 и R4 = R — R2 (при внутреннем сопряжении, рис.13). Точка О является центром искомой дуги окружности радиуса R.

Точки сопряжения С1 и С2 будут находиться на линии центров О1 О и О2 О

(рис.12) или на продолжении линии центров (рис.13).

При нахождении радиуса внешне–внутреннего сопряжения вспомогательные дуги проводятся радиусами R3 = R — R1 из центра О1 и

R4 = R + R2 из центра О2 (рис.14).

Сопряжение окружности с прямой по дуге радиуса R

Из центра О1 проводится дуга радиусом R2 = R1 + R и прямая,

параллельная заданной, на расстоянии R. Пересечение вспомогательной дуги окружности и прямой определит искомый центр О. Точка сопряжения дуг С1

лежит на линии центров О1 О, а прямой и дуги сопряжения С – на перпендикуляре, проведенном к заданной прямой из центра О (рис.15).

O2 O1

R4 = R2 + R

R3 = R1

С 1

С2

R3 = R — R1
	R — R2

С1

O 2

R 3 = R — R 1 O

R2 = R+R1

НОРМАЛЬНЫЕ УГЛЫ
(ГОСТ 8908-81)

&nbsp Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.

НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ
(ГОСТ 8593-81)

&nbsp Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.

&nbsp Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ
(ГОСТ 9953-82)

&nbsp Стандарт распространяется на укороченные инструментальные конусы Морзе.

&nbsp *z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения.
&nbsp ** размеры для справок.

Обозначение конуса	Конус Морзе	D	D 1	d	d 1	l 1	l 2	a, не более	b	c
B7	0	7,067	7,2	6,5	6,8	11,0	14,0	3,0	3,0	0,5
B10 B12	1	10,094 12,065	10,3 12,2	9,4 11,1	9,8 11,5	14,5 18,5	18,0 22,0	3,5 3,5	3,5 3,5	1,0 1,0
B16 B18	2	15,733 17,780	16,8 18,0	14,5 16,2	15,0 16,8	24,0 32,0	29,0 37,0	5,0 5,0	4,0 4,0	1,5 1,5
B22 B24	3	21,793 23,825	22,0 24,1	19,8 21,3	20,5 22,0	40,5 50,5	45,5 55,5	5,0 5,0	4,5 4,5	2,0 2,0
B32	4	31,267	31,6	28,6	—	51,0	57,5	6,5	—	2,0
B45	5	44,399	44,7	41,0	—	64,5	71,0	6,5	—	2,0
Размеры D 1 и d являются теоретическими, вытекающими соответственно из диаметра D и номинальных размеров а и l 1

КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ
И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ
(ГОСТ 25557-2006)

Тип конуса	Метрический		Морзе							Метрический
Обозн.	4	6	0	1	2	3	4	5	6	80	100	120	160	200
D	4,0	6,0	9,045	9,065	17,78	23,825	31,267	44,399	63,348	80	100	120	160	200
D 1	4,1	6,2	9,2	12,2	18,0	24,1	31,6	44,7	63,8	80,4	100,5	120,6	160,8	201,0
d*	2,9	4,4	6,4	9,4	14,6	19,8	25,9	37,6	53,9	70,2	88,4	106,6	143	179,4
d 1	—	—	—	М6	М10	М12	М16	М20	М24	М30	М36	М36	М48	М48
d 4 max	2,5	4,0	6,0	9,0	14,0	19,0	25,0	35,7	51,0	67,0	85,0	102,0	138,0	174,0
l min	—	—	—	16,0	24,0	24,0	32,0	40,0	47,0	59,0	70,0	70,0	92,0	92,0
l 1	23,0	32,0	50,0	53,5	64,0	81,0	102,5	129,5	182,0	196,0	232,0	268,0	340,0	412,0
l 2	25,0	35,0	53,0	57,0	69,0	86,0	109,0	136,0	190,0	204,0	242,0	280,0	356,0	432,0
l 11	—	—	—	4,0	5,0	5,5	8,2	10,0	11,5	—	—	—	—	—
* — размер для справок. — угол конусов Морзе №0-№5 соответствует углу укороченных конусов Морзе; №6 — 1:19,180 = 0,05214 — угол метрических конусов — 1:20 = 0,05.

&nbsp Профиль резьбового отверстия соответствует отверстию центровому форма Р по ГОСТ ГОСТ 14034-74 .

&nbsp В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.

&nbsp В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:

BI — внутренний конус с пазом;
BE — наружный конус с лапкой;
AI — внутренний конус с отверстием по оси;
АЕ — наружный конус с резьбовым отверстием по оси;
BIK — внутренний конус с пазом и отверстием для подачи СОЖ;
ВЕК — наружный конус с лапкой и отверстием для подачи СОЖ;
AIK — внутренний конус с отверстием по оси и отверстием для подачи СОЖ;
АЕК — наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ
(ГОСТ 25557-2006)

КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7: 24
(ГОСТ 15945-82)

&nbsp Допуски конусов внутренних и наружных конусностью 7:24 по ГОСТ 19860-93.

КОНУСЫ ИНСТРУМЕНТОВ
Предельные отклонения угла конуса и допуски формы конусов
(ГОСТ 2848-75)

&nbsp Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.

&nbsp Примечания:
&nbsp 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних.
&nbsp 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.

&nbsp Пример обозначения конуса Морзе 3, степени точности АТ8:

Морзе 3 АТ8 ГОСТ 25557-2006

&nbsp То же метрического конуса 160, степени точности АТ7:

Метр. 160 АТ7 ГОСТ 25557-2006

&nbsp То же укороченного конуса В18, степени точности АТ6:

Морзе В18 АТ6 ГОСТ 9953-82

Похожие документы:

ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля
ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры
ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры
ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры
ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения

Конусность и уклон

На изображениях конических элементов деталей размеры могут быть проставлены различно: диаметры большего и меньшего оснований усеченного конуса и его длина; угол наклона образующей (или угол конуса) или величина конусности и диаметр основания, длина и т.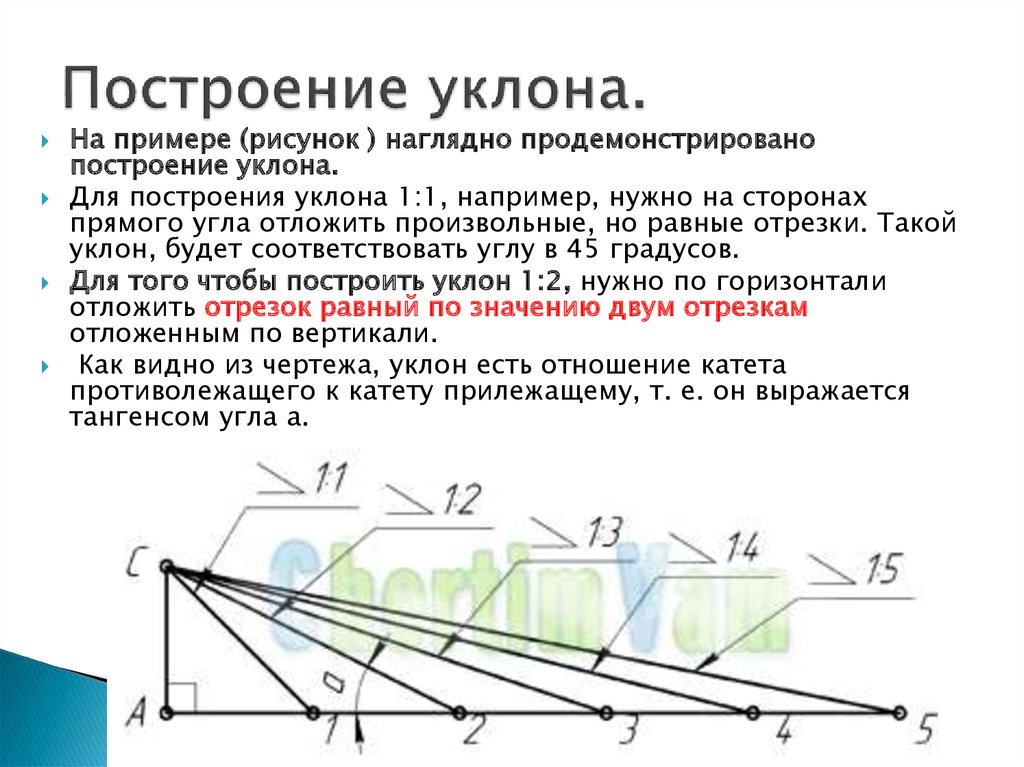 п.

Конусность

Отношение разности диаметров двух поперечных сечений конуса (D-d. ) к расстоянию между ними (l ) (рис. 6.39, а ) называется конусностью (К ): К = (D – d )/l.

Рис. 6.39.

Например, конический элемент детали с диаметром большего основания 25 мм, диаметром меньшего основания 15 мм, длиной 50 мм будет иметь конусность К = (D – d )/l = (25 – 15)/50 = 1/5 = 1:5.

При проектировании новых изделий применяются величины конусности, установленные ГОСТ 8593–81: 1:3; 1:5; 1:7; 1:8; 1:10; 1:12; 1:15; 1:20; 1:30. Стандартизированы также величины конусности, которые имеют элементы деталей с часто встречающимися углами между образующими конуса: углу 30° соответствует конусность 1:1,866; 45° – 1:1,207; 60° – 1:0,866; 75° – 1:0,652; углу 90° – 1:0,5. В чертежах металлорежущих инструментов часто конусность определяется надписью, указывающей номер конуса Морзе. В этих случаях размеры конических элементов устанавливают по ГОСТ 10079–71 и др.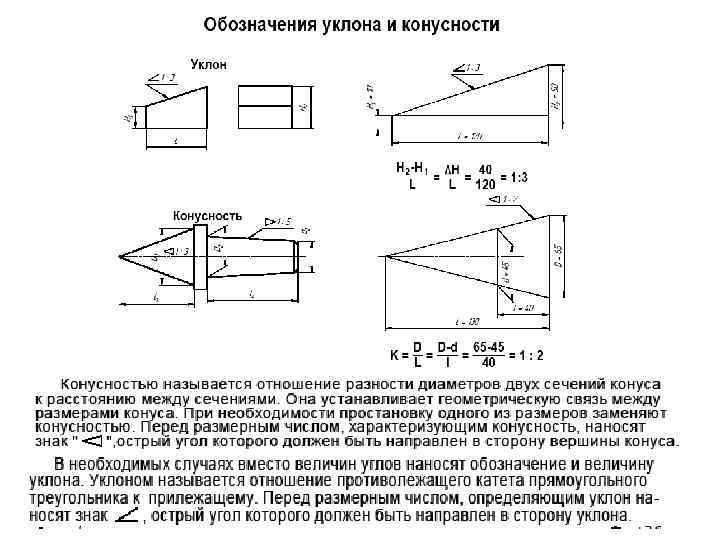

На чертежах конусность наносят согласно правилам ГОСТ 2.307–2011. Перед размерным числом, определяющим величину конусности, наносят условный знак в виде равнобедренного треугольника, острие которого направлено в сторону вершины конуса.

Знак и цифры, указывающие величину конусности, располагают на чертежах параллельно геометрической оси конического элемента.

Они могут быть проставлены над осью (рис. 6.39, 6 ) или на полке (рис. 6.39, в). В последнем случае полка соединяется с образующей конуса с помощью линии выноски, заканчивающейся стрелкой.

Уклон

Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис.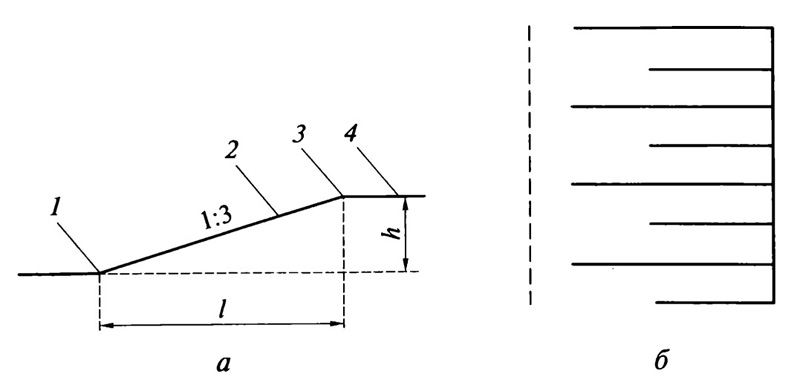 6.40, б ). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.

Рис. 6.40.

На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.

Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).

Рис. 6.41.

При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.

Рис. 6.42.

Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.

Тема 2. Геометрические построения

2.1. Уклон и конусность

Наклонные прямые элементы изображенного предмета характеризуются углами наклона к горизонтальной прямой, или уклоном. Уклоном i прямой АВ относительно прямой АС (рис. 2.1) называется отношение превышения прямой к горизонтальной ее проекции i = ВС/АС = tgα. Уклоны выражают отношением чисел (1:10) или в процентах (10%), а также десятичными дробями, например 0,09. На чертежах уклон обозначается знаком , который ставится перед размерным числом, определяющим уклон, параллельно основному направлению. Вершина угла направлена в сторону уклона. Обозначение уклона наносят на полке линии-выноски или непосредственно над линией контура.

Если предмет имеет коническую форму, то на чертеже указывают степень конусности. Конусностью К называется отношение разности диаметров двух нормальных сечений конуса (D, d) к расстоянию между ними (l) (рис. 2.2, а). К= (D — d)/l = 2tgα, следовательно, К— 2i. Перед размерным числом, характеризующим конусность, ставят условный знак о в виде равнобедренного треугольника, острый угол которого направлен в сторону вершины конуса (рис. 2.2, б).

Задание 5. Вычертить заготовку для пробкового крана по одному из вариантов. Определить конусность и проставить размеры. Построить деталь с коническим элементом.

Варианты индивидуальных заданий приведены на рис. 2.3 и 2.4 и в табл. 2.1.

Указания к выполнению задания 5. Работа выполняется в рабочей тетради.

По данным размерам и величине конусности выполните изображения детали. Обозначьте конусность. Подсчитайте размеры, отмеченные звездочкой: d* для пробки, l* для заглушки и D* для втулки.

Задание 6. Вычертить фланец в М 1:1 по данному варианту

Варианты индивидуальных заданий приведены на рис. 2.5 ив табл. 2.2.

Рис. 2.1. Построение и обозначение уклона

Рис. 2.3. Заготовка для пробкового крана

Рис. 2.4. Изображение детали: а – заглушка; б – втулка

Рис. 2.2. Построение конусности (а) и обозначение ее на чертежах (б)

Таблица 2.1. Варианты Задания 5

Рис. 2.5. Фланец

Таблица 2.2. Варианты Задания 6

Задание 7. Вычертить контуры деталей, применяя правила построения сопряжений

Указания к выполнению задания 7. При выполнении сопряжений должны учитываться три элемента построения: радиус дуги перехода, центр дуги перехода и точка сопряжения. Задается один из этих элементов, например радиус, остальные размеры должны быть найдены. Все построения на чертеже сохраните и обведите тонкими сплошными линиями, точки сопряжения отметьте кружочком. Пример оформления задания показан на рис. 2.6.

Варианты задания возьмите из рис. 2.7—2.10.

Задание 8. Вычертить контуры деталей, применяя правила деления окружностей на равные части

Варианты задания возьмите из рис. 2.11.

Рис. 2.7. Варианты к Заданию 7

Рис. 2.11. Варианты к Заданию 8

Рис. 2.12. Проведение кривой по лекалу

Задание 9. Построение лекальных кривых

Указания к выполнению задания 9. По исходным данным постройте указанные лекальные кривые. Точки построения допускается не отмечать. На рис. 2.12 показано проведение лекальной кривой по лекалу.

На рис. 2.13 показан пример построения эллипса по осям, а на рис. 2.14, а, б – построение параболы.

Задания возьмите из табл. 2.3 и рис. 2.15

Задание 9А. Построение циркульных кривых

Вычертите несколько циркульных кривых и спираль Архимеда.

Задание возьмите из табл. 2.4 и рис. 2.16.

Задание 10. Постройте профиль прокатной стали – двутавра или швеллера в масштабе 1:1 с построением уклонов их полок

Указания к выполнению задания 10. При вычерчивании профилей двутавра и швеллера все размеры берут из табл. 2.5 и 2.6 индивидуальных заданий, а на чертежах вместо буквенных обозначений ставят размерные числа. После построения уклона полок строят сопряжения, наносят штриховку в сечениях и размерные числа.

Индивидуальные задания приведены на рис. 2.17 и 2.18, в табл. 2.5 и 2.6

На рис. 2.19 показано построение сопряжения сторон углов, а на рис. 2.20 дан пример оформления задания 10.

Таблица 2.3. Варианты Задания 9

Рис. 2.13. Построение эллипса по осям

Рис. 2.14. Построение параболы по одной точке, вершине и оси (а), чертеж вазы с параболическим контуром (б)

Рис. 2.15. Выполнение нескольких лекальных кривых

Рис. 2. 16. Построение циркульных кривых

Таблица 2.4. Варианты Задания 9А

Рис. 2.17. Пример задания на построение двутавра

Рис. 2.18. Пример задания на построение швеллера

Таблица 2.5. Заданий на двутавр по ГОСТ 8239-72

Таблица 2.6. Варианты Заданий на швеллер по ГОСТ 8240-72

Рис. 2.19. Сопряжение сторон углов: а – прямого; б – острого; в – тупого; г – построение профиля прокатной стали

Рис. 2.10. Пример оформления Задания 10

Контрольная работа № 1 на сопряжение

На бумаге формата А4 вычертите изображения вазы согласно предложенным вариантам. Задания возьмите из рис. 2.21.

Рис. 2.21. Задания на выполнение сопряжении

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Как найти наклон перпендикулярной линии

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

ACT Math Help » Алгебра » Координатная плоскость » Линии » Перпендикулярные линии » Как найти наклон перпендикулярной линии

Каков наклон любой прямой, перпендикулярной 2 y = 4 x +3 ?

Possible Answers:

– 4

– ½

Correct answer:

– ½

Объяснение:

Сначала мы должны решить уравнение для y , чтобы определить наклон:0911 x , мы знаем, что наклон этой линии имеет значение 2. Чтобы точно определить наклон любой линии, перпендикулярной этой, мы берем обратное отрицательное значение:

наклон = м , перпендикулярный наклон = – ¹ / _M

Slope = 2, перпендикулярный уклон = — ¹ /₂

. (1,1)?

Possible Answers:

2x + 3y = 1

x + 2y — 3

x – 2y = -1

3x + 2y = 1

Correct answer:

x – 2y = -1

Пояснение:

Найдите наклон данной линии. Перпендикулярный наклон будет противоположным обратным исходному наклону. Используйте форму пересечения наклона (y = mx + b) и подставьте заданную точку и новый наклон, чтобы найти пересечение, b. Вернемся к стандартной форме уравнения: ax + by = c.

Отчет о ошибке

Каков наклон линии, перпендикулярной линии, данной уравнением

6x -9y +14 = 0

. 2/3

-3/2

-2/3

Правильный ответ:

-3/2

Объяснение:

Сначала перестройте уравнение так, чтобы оно было в форме пересечения наклона, в результате чего у=2/3 х + 14/9 . Наклон этой линии равен 2/3, поэтому наклон перпендикулярной линии будет иметь обратное значение, противоположное наклону, равное -3/2.

Сообщить об ошибке

Каков наклон линии, перпендикулярной линии, представленной уравнением y = -2x+3?

Возможные ответы:

1/2

2/3

-2/3

-1/2

09 Правильный ответ:0926

1/2

Пояснение:

Перпендикулярные линии имеют наклоны, противоположные друг другу. В этом случае наклон первой линии равен -2. Обратная величина -2 равна -1/2, поэтому обратная величина равна 1/2.

Сообщить об ошибке

Найти наклон прямой, перпендикулярной прямой y = –3x – 4.

Возможные ответы:

1/4

–3

1/3

Правильный ответ:

1/3

Пояснение:

Сначала мы должны найти наклон данной линии. Наклон y = –3x – 4 равен –3. Наклон перпендикулярной линии является обратной отрицательной величиной. Это означает, что вы меняете знак наклона на противоположный: в данном случае на 3. Затем найдите обратную величину, поменяв местами знаменатель и числитель, чтобы получить 1/3; поэтому наклон перпендикулярной линии равен 1/3.

Сообщить об ошибке

Каков наклон линии, перпендикулярной следующему:

Возможные ответы:

Правильный ответ: 90 90 Объяснение:

В вопросе линия представлена в виде точка-наклон y – y ₁ = m(x – x ₁ ), где m — уклон. Следовательно, наклон исходной линии равен 1/2. Прямая, перпендикулярная другой, имеет наклон, который является отрицательной обратной величиной наклона другой прямой. Отрицательная обратная величина исходной строки равна 9.0911 – 2 и, таким образом, представляет собой наклон его перпендикулярной линии.

Сообщить об ошибке

Линия определяется следующим уравнением:

Каков наклон линии, перпендикулярной указанной выше линии?

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение прямой где – наклон.

Измените уравнение, чтобы оно соответствовало этому:

Для перпендикулярной линии наклон является отрицательным обратным;

поэтому

Сообщить об ошибке

Какая из следующих прямых перпендикулярна прямой, проходящей через точки?

Возможные ответы:

Правильный ответ:

Пояснение:

Во-первых, вы должны найти наклон данной вам линии. Помните, что уклон рассчитывается:

Таким образом, для наших данных это:

Теперь перпендикулярный наклон к этому равен противоположному и обратному . Значит, так и должно быть. Это верно только для уравнения

. Чтобы узнать это, решите уравнение для формата . Это позволит вам очень быстро найти уклон, так как он есть . Сначала прибавьте к обеим сторонам:

Затем разделите все на:

Вам просто нужно обратить внимание на термин. Это сводится к , а это как раз то, что вам нужно!

Сообщить об ошибке

Каков наклон прямой, перпендикулярной уравнению:

Возможные ответы:

Правильный ответ:

9 Объяснение:

Перпендикулярные линии имеют наклоны, произведение которых .

и, следовательно, ответ

Сообщить об ошибке

Каков наклон линии, перпендикулярной линии , которая проходит через и ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти наклон перпендикулярной линии, мы берем обратную величину известного наклона, где .

РубрикаРазное