Пропорции при – Пропорции | Формулы с примерами
Пропорции | Формулы с примерами
Что такое пропорция?
Определение
Пропорция — это верное равенство двух отношений.
Где a ? 0, b ? 0, c ? 0, d ? 0.
a и d — называют крайними членами пропорции;
b и c — называют средними членами пропорции.
| 3 | = | 18 | или 3 : 5 = 18 : 30; |
| 5 | 30 |
| 7 | = | 21 | или 7 : 3 = 21 : 9; |
| 3 | 9 |
| 12 | = | 48 | или 12 : 15 = 48 : 60. |
| 15 | 60 |
Основное свойство пропорции
СвойствоПроизведение крайних членов пропорции равно произведению ее средних членов.
| 12 | = | 24 | , значит 12 • 8 = 4 • 24; |
| 4 | 8 |
| 11 | = | 33 | , значит 11 • 21 = 7 • 33; |
| 7 | 21 |
| 23 | = | 69 | , значит 23 • 42 = 14 • 69. |
| 14 | 42 |
Обратное свойство
Свойство Пример| 11 • 4 = 2 • 22 значит, | 11 | = | 22 | ; |
| 2 | 4 |
| 21 • 6 = 42 • 3 значит, | 21 | = | 42 | ; |
| 3 | 6 |
| 33 • 21 = 7 • 99 значит, | 33 | = | 99 | . |
| 7 | 21 |
Производные пропорции
Правило Пример
Пример | 4 | = | 8 | или | 7 | = | 14 | или | 8 | = | 17 | или | 4 | = | 7 | ; |
| 7 | 14 | 4 | 8 | 4 | 8 | 14 |
| 5 | = | 10 | или | 6 | = | 12 | или | 10 | = | 12 | или | 5 | = | 6 | ; |
| 6 | 12 | 5 | 10 | 5 | 6 | 10 | 12 |
| 9 | = | 18 | или | 3 | = | 6 | или | 6 | = | 18 | или | 9 | = | 3 | . |
| 3 | 6 | 9 | 18 | 3 | 9 | 18 | 6 |
Правило
! По трем известным членам пропорции всегда можно найти
ее неизвестный член.
| 15 | = | x | , значит x = | 15 • 14 | = 15 • 2 = 30; |
| 7 | 14 | 7 |
| 21 | = | x | , значит x = | 21 • 9 | = 21 • 3 = 63; |
| 3 | 9 | 3 |
| 33 | 99 | , значит x = | 4 • 99 | = 4 • 3 = 12. | |
| 4 | x | 33 |
Отношения
Определение
Отношением двух чисел a и b называется их частное a : b.
Показывает во сколько раз a больше b или какую часть число a составляет от b.1
Примеры отношений
Пример 1
Отношение числа 16 к числу 4 равно 16 : 4 = 4, т.е. 16 в 4 раза больше чем,
чем 4.
Пример 2
Отношение числа 4 к числу 12 равно 4 : 12 = 13, т.е. 4 составляет треть
от числа 12.
Масса стакана с жидкостью равна 440г. Стакан весит 40г. Какую часть
всей массы составляет масса стакана? Во сколько раз масса стакана с
жидкостью больше массы жидкости?
Решение:
Масса стакана составляет 40 : 440 = 1 11 часть полной массы.
Масса жидкости равна 440 — 40 = 400г; масса стакана с жидкостью больше массы самой жидкости в 440 : 400 = 1,1 раза.
formula-xyz.ru
Как составить и рассчитать пропорцию: онлайн калькулятор
Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 | ||||
Основные свойства пропорции
a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
shpargalkablog.ru
Составить пропорцию
Составить пропорцию. В этой статье хочу поговорить с вами о пропорции. Понимать, что такое пропорция, уметь составлять её – это очень важно, она действительно спасает. Это вроде бы маленькая и незначительная «буковка» в большом алфавите математики, но без неё математика обречена быть хромой и неполноценной. Для начала напомню, что такое пропорция. Это равенство вида:
что тоже самое (это разная форма записи).
Пример:
Говорят – один относится к двум также, как четыре относится к восьми. То есть это равенство двух отношений (в данном примере отношения числовые).
Основное правило пропорции:
a:b=c:d
произведение крайних членов равно произведению средних
то есть
a∙d=b∙c
*Если какая-либо величина в пропорции неизвестна, ее всегда можно найти.
Если рассматривать форму записи вида:
то можно использовать следующее правило, его называют «правило креста»: записывается равенство произведений элементов (чисел или выражений) стоящих по диагонали
a∙d=b∙c
Как видите результат тот же.
Если три элемента пропорции известны, то мы всегда можем найти четвёртый.
Именно в этом суть пользы и необходимость пропорции при решении задач.
Давайте рассмотрим все варианты, где неизвестная величина х находится в «любом месте» пропорции, где a, b, c – числа:
Величина стоящая по диагонали от х записывается в знаменатель дроби, а известные величины стоящие по диагонали записываются в числитель, как произведение. Его запоминать не обязательно, вы и так всё верно вычислите, если усвоили основное правило пропорции.
Теперь главный вопрос, связанный с названием статьи. Когда пропорция спасает и где используется? Например:
1. Прежде всего это задачи на проценты. Мы рассматривали их в статьях «Задачи на проценты. Часть 1!» и «Задачи на проценты. Часть 2!».
2. Многие формулы заданы в виде пропорций:
> теорема синусов
> отношение элементов в треугольнике
> теорема тангенсов
> теорема Фалеса и другие.
3. В задачах по геометрии в условии часто задаётся отношение сторон (других элементов) или площадей, например 1:2, 2:3 и прочие.
4. Перевод единиц измерения, причём пропорция используется для перевода единиц как в одной мере, так и для перевода из одной меры в другую:
— часы в минуты (и наоборот).
— единицы объёма, площади.
— длины, например мили в километры (и наоборот).
— градусы в радианы (и наоборот).
здесь без составления пропорции не обойтись.
Ключевой момент в том, что нужно правильно установить соответствие, рассмотрим простые примеры:
Необходимо определить число, которое составляет 35% от 700.
В задачах на проценты за 100% принимается та величина, с которой сравниваем. Неизвестное число обозначим как х. Установим соответствие:
Можно сказать, что семисот тридцати пяти соответствует 100 процентов.
Иксу соответствует 35 процентов. Значит,
700 – 100%
х – 35 %
Решаем
Ответ: 245
Переведём 50 минут в часы.
Мы знаем, что одному часу соответствует 60 минут. Обозначим соответсвие — x часов это 50 минут. Значит
1 – 60
х – 50
Решаем:
То есть 50 минут это пять шестых часа.
Ответ: 5/6
Николай Петрович проехал 3 километра. Сколько это будет в милях (учесть, что 1 миля это 1,6 км)?
Известно, что 1 миля это 1,6 километра. Число миль, которые проехал Николай Петрович примем за х. Можем установить соответствие:
Одной миле соответствует 1,6 километра.
Икс миль это три километра.
1 – 1,6
х – 3
Ответ: 1,875 миль
Вы знаете, что для перевода градусов в радианы (и обратно) существуют формулы. Я их не записываю, так как запоминать их считаю излишним, и так вам в памяти приходится держать много информации. Вы всегда сможете перевести градусы в радианы (и обратно), если воспользуетесь пропорцией.
Переведём 65 градусов в радианную меру.
Главное это запомнить, что 180 градусов это Пи радиан.
Обозначим искомую величину как х. Устанавливаем соответствие.
Ста восьмидесяти градусам соответствует Пи радиан.
Шестидесяти пяти градусам соответствует х радиан.
Если записать отношение в общем виде, то получится
То есть, если необходимо перевести градусы в радианы, то подставляете в эту пропорцию градусы и вычисляете радианы; если необходимо перевести радианы в градусы, то подставляете радианы и вычисляете градусы.
Можете изучить статью по этой теме на блоге. Материал в ней изложен несколько по иному, но принцип тот же. На этом закончу. Обязательно будет ещё что-нибудь интересненькое, не пропустите!
Если вспомнить само определение математики, то в нём есть такие слова: математика изучает количественные ОТНОШЕНИЯ (ОТНОШЕНИЯ — здесь ключевое слово). Как видите в самом определении математики заложена пропорция. Вообщем, математика без пропорции это не математика!!!
Всего доброго!
С уважением, Александр
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Золотое сечение и пропорции при создании предметов мебели
Золотое сечение было известно еще в древней Греции. В дошедшей до нас античной литературе упоминание о нем впервые встречается в «Началах» Эвклида.
В XV-XVI вв. среди ученых и художников усилился интерес к золотому сечению в связи с его применением как в геометрии, так и в искусстве, особенно архитектуре. В настоящее время эта пропорция также применяется ваятелями и зодчими в зависимости от характера создаваемого ими художественного образа.
Золотое сечение (гармоничное деление, деление в крайнем и среднем отношении) — это деление отрезка на две части, при котором большая его часть является средней пропорциональной между всем отрезком и меньшей частью (рис. 161),
Рис. 161. Деление отрезка на части в золотом сечении.
т. е. а:х = х:(а — х).
Чтобы найти х, возьмем квадратное уравнение:
х2 + ах — а2 = 0, решение которого дает
х = а:2 (√5 — 1) ≈ 0,62а.
Это значит, что части золотого сечения составляют приблизительно 62 и 38% всего отрезка1.
1 Дальнейшими исследованиями введена функция золотого сечения, равная:
(√5:2):1 = (2∙24):2 = 1,12.
Золотое сечение может быть выражено в виде дроби: 1:1; 1:2; 2:3; 3:5; 5:8; 8:13; 13:21; 21:34; 34:55; 55:89 и т. д., где 1,1; 2,3; 5,8; 13,21 и т. д. — так называемый ряд Фибоначчи, представляющий такую последовательность чисел, в которой каждый член, начиная с третьего, равен сумме двух ему предшествующих. Если строить отрезки в золотом сечении, то величина каждого предыдущего отрезка будет равна сумме двух последующих.
Рис. 162. Схема деления отрезка на части в золотом сечении.
Примеры деления квадрата в золотом сечении показаны на рис. 163.
Рис. 163. Схема деления квадрата в золотом сечении.
Метрическая система с ее десятичными подразделениями не совсем точно совпадает с антропометрическими данными в размерах человеческого тела, поэтому многие архитекторы для проектирования ряда предметов мебели разрабатывают модулоры, объединяющие в себе обе зависимости.
На рис. 164 показано сложное построение прямоугольников на основе золотого сечения. Развивающуюся систему прямоугольников строят на отношениях ряда √2, √3, √4, √5 и т. д. Гармоничная связь величин образуется благодаря их свойству распадаться на элементы, повторяющие строение целого при сохранении кратных соотношений сторон.
Рис. 164. Построение системы прямоугольников с отношением сторон 1:√2, 1:√3, 1:√4, 1:√5 и т.д.
Иной закономерностью обладают величины, участвующие в пропорции, которые не соизмеримы с единицей, т. е. 1:√2; 1:√3 и др. При построении фигур по ним возникает пропорционально убывающий или возрастающий ряд, который даст динамичную композицию.
Связь пропорции √5 и золотого сечения показана на рис. 165. Этому прямоугольнику присуще особое свойство. При членении его полуокружностью по краям образуются прямоугольники в золотом сечении (0,618:1), а посередине — квадрат или два прямоугольника в золотом сечении (0,618:1 и 1:618). Если к первоначальной фигуре прибавить квадрат, то получаются два прямоугольника золотого сечения.
Рис. 165. Связь пропорций √5 и золотого сечения.
Рис. 166 иллюстрирует свойство прямоугольника с размерами сторон 1 и √2 сохранять первоначальную пропорцию при делении его пополам.
Рис. 166. Свойство прямоугольника сохранять первоначальную пропорцию при делении пополам.
Геометрически подобными будут фигуры, построенные на основе ряда натуральных чисел (1, 2, 3, 4, 5 и т. д.) (рис. 167).
Рис. 167. Геометрически подобные фигуры, построенные на основе ряда натуральных чисел.
Если нужно перевести рисунок в нужную соподчиненность размеров, то пользуются пропорциональным циркулем. Он делится на две части и закрепляется подвижным шарниром. Если шарнир закрепить строго на 1/2 длины циркуля, то размеры с обеих сторон при любом растворе будут всегда равны (рис. 168, а), т. е. а = b и c = d. Если шарнир закрепить в точке неравных величин, то расстояния между его концами будут разные, но пропорциональные друг другу (рис. 168, б), т. е. a:b = c:d. Исходя из нужной пропорциональности, шарнир закрепляют в определенной точке. На рис. (168, в) показан пропорциональный циркуль, закрепленный в золотом сечении.
Наиболее ясно и убедительно пропорциональность (в мебели, орнаменте и т. д.) выражается при наличии трех частей. Если предмет состоит из четырех и более частей, то ясность пропорциональной соразмерности слабеет, разрушается.

Рис. 168. Пропорциональный циркуль: а — закрепленный на середине длины, б — закрепленный произвольно, в — закрепленный в золотом сечении
www.drevesinas.ru
схема. Идеальные пропорции лица :: SYL.ru
Портрет передает не только внешние характеристики лица, но и отражает внутренний мир человека, его отношение к реальности и эмоциональное состояние в определенный момент времени. Фактически, портрет, как и любая другая жанровая картина, — это расположение линий, форм и цветов на холсте или бумаге так, что их конечное сочетание повторяет форму человеческого лица.
Звучит почти как волшебство? Чтобы правильно располагать на бумаге те самые линии, формы и оттенки, нужно прежде всего изучить пропорции лица человека (при рисовании портрета их необходимо соблюдать в обязательном порядке) и их зависимость от движений, направления и формы головы.

Что такое портрет?
Вне зависимости от уровня мастерства, работа над ним пугает любого художника. Замечательный живописец Джон Сингер Сарджент дал портрету две характеристики, с которыми согласится каждый художник:
- «Каждый раз, рисуя портрет, особенно на заказ, я теряю друга».
- «Портрет – это картина, на которой в конечном итоге губы выглядят как-то не так».
Портрет – один из самых сложных жанров рисунка и живописи. Причиной является то, что художник часто работает на заказ, а давление со стороны мешает творческому процессу. Портрет в представлении заказчика зачастую отличается от того, что создает художник. Кроме того, для работы над изображением человеческого лица необходимы специальные знания и изрядная доля терпения.
Зачем изучать пропорции
Пропорции нужны для того, чтобы понять, как объекты расположены относительно друг друга в размерном, плоскостном и промежуточном соотношении. Если для портрета важна хоть небольшая доля реализма, без знания пропорций этого не добиться. С другой стороны, абстрактные портреты никто не отменял.
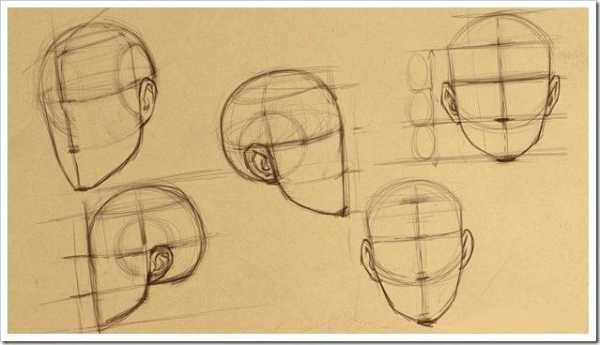
Знание пропорций помогает передавать не только черты лица, но и эмоции и мимику человека. Зная зависимость изменения внешнего вида от положения головы, эмоционального состояния модели и освещения, художник может перенести на холст характер и настроение человека, тем самым создавая предмет искусства. Но для этого необходимо знать правильные пропорции лица и уметь строить композицию в соответствии с правилами.
Идеальные пропорции
В период Высокого Возрождения Рафаэль создавал картины, которые считались эталоном совершенства. Фактически все сегодняшние идеальные пропорции берут свое начало в овале лиц Мадонн Рафаэля.
Если провести вертикальную линию в самом центре лица и разделить ее на три части — от линии роста волос до бровей, от бровей до кончика носа и от кончика носа до подбородка, то у идеального лица эти части будут равны. На представленном ниже рисунке показаны идеальные пропорции лица человека, схема рисования и построения идеального овала лица, а также соотношение основных черт. Стоит учесть, что идеал мужского лица характеризуется более угловатыми чертами, но, несмотря на это, основное их расположение соответствует представленной схеме.
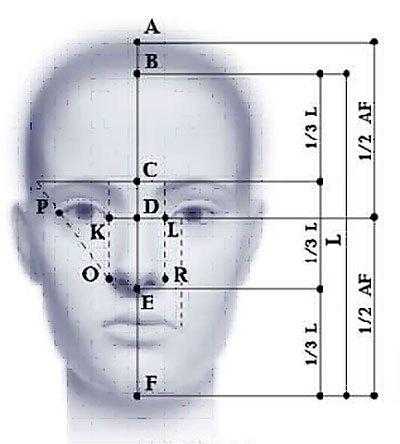
Исходя из данной схемы, идеальные пропорции лица при рисовании портрета соответствуют следующей формуле:
- BC = CE = EF.
- AD = DF.
- OR = KL = PK.
Форма лица
Правильно построенные пропорции лица человека при рисовании портрета зависят во многом и от формы этого лица. Рафаэль, создал совершенный овал, а природа не ограничивает совершенство лишь одной геометрической формой.
Вероятно, изучить построение пропорций и их изменение при движении удобнее всего на идеально овальном лице, для этого существует масса способов и приемов, которые будут рассмотрены ниже, но суть портрета не в создании идеала, а в изображении человека со всеми его особенностями и несовершенствами. Именно поэтому важно знать, какой может быть форма лица и как она влияет на построение пропорций при рисовании портретов.
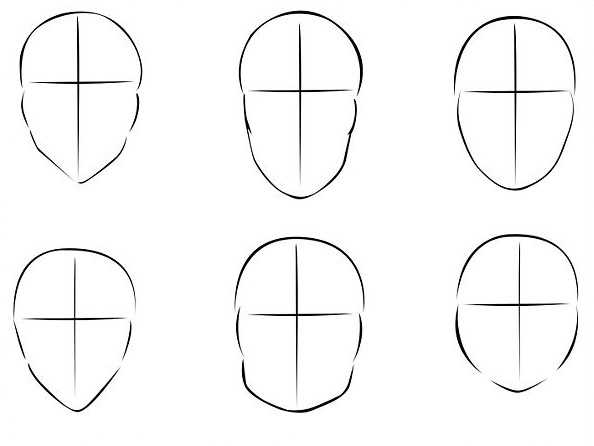
Существует две категории лиц – округлые и угловатые, в свою очередь, эти категории разделяются на восемь основных форм.
Округлые формы лиц
Удлиненное лицо обладает закругленными формами линии роста волос и подбородка. Вертикальная средняя линия лица гораздо длиннее горизонтальной. Характеристикой удлиненных лиц обычно является высокий лоб и большое расстояние между верхней губой и основанием носа. Обычно ширина лба примерно равна ширине скул.
Овальное лицо схоже по форме с перевернутым острой стороной вниз яйцом. Самой широкой его частью являются скулы, затем идет чуть менее широкий лоб и сравнительно узкая челюсть. Длина овального лица немного больше его ширины.
Круглое лицо характеризуется практически равными средними линиями вертикального и горизонтального сечения лица. Широкие скулы сглаживаются плавной округлой линией подбородка.
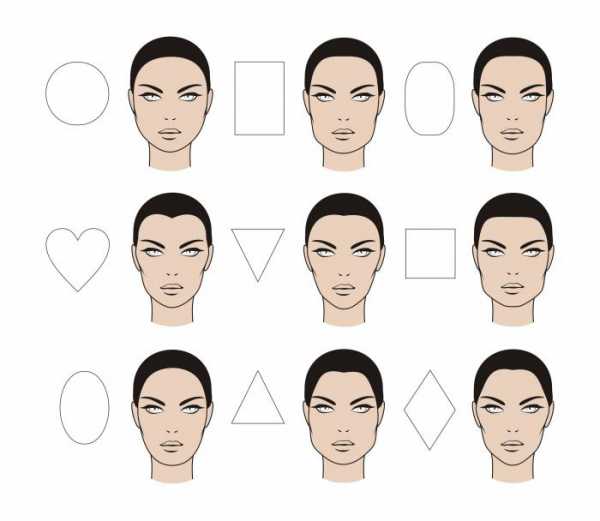
Угловатые формы лиц
Прямоугольное лицо характеризуется широкой челюстью, подчеркнутой угловатым подбородком и прямой линией роста волос. Средняя линия вертикального сечения намного длиннее горизонтальной. Ширина лба человека с прямоугольным лицом примерно равна ширине скул.
Треугольное отличается от сердцеобразного только линией роста волос, у треугольного она прямая. Характерная черта этой формы лиц – высокие скулы и очень узкий, острый подбородок, в то время когда скулы практически так же широки, как и лоб. Вертикальная линия сечения треугольного лица обычно чуть длиннее горизонтальной.
Квадратная форма свойственна лицам с низкими, широкими скулами и угловатым подбородком. Длина квадратного лица равна его ширине.
Трапециевидное определяется широкой челюстью, низкими скулами и узким лбом. Обычно на таком лице подбородок угловат и широк, а скулы намного шире лба.
Ромбовидную форму лицу придают пропорционально узкие лоб и подбородок, причем последний обычно заострен. Высокие скулы – самая широкая часть ромбовидного лица, а его горизонтальное сечение гораздо меньше вертикального.
Правильное построение лица
Правильное построение при рисовании портрета основывается на измерении черт лица модели и расстояния между ними. Каждый портрет индивидуален, так же как нет и двух абсолютно одинаковых лиц, за исключением близнецов. Формулы вычисления пропорций дают лишь основные советы, следуя которым можно намного облегчить процесс рисования.
Для создания собственных персонажей или рисования лиц по памяти крайне важно знать правильную передачу пропорций. Здесь важно помнить, что форма головы гораздо сложнее перевернутого яйца или овала, а потому стоит следовать правилам, чтобы избежать глаз на лбу или слишком маленького рта.
Очертания лица
Для начала рисуем круг – это будет широкой частью черепа. Как известно, основные черты лица занимают место под кругом. Чтобы примерно определить их место, делим круг пополам вертикально и линию продолжаем вниз так, чтоб нижнее очертание окружности делило ее ровно пополам. Низ линии будет подбородком. От боков круга к «подбородку» нужно провести линии, которые станут предварительными очертаниями скул и щек.
Если портрет рисуется с лица модели или по памяти, то можно несколькими легкими линиями подкорректировать форму, определить примерную ширину подбородка и линию роста волос. Стоит обратить внимание, что волосы на портрете будут занимать некоторую часть круга, который был нарисован в самом начале.
Глаза и брови
У основания круга проводим горизонтальную линию, перпендикулярно первой. На этой линии располагаются глаза. Именно на ней, не выше, как бы ни хотелось! Горизонтальную линию нужно разделить на пять равных частей – каждая из них равна ширине глаза. Центральная часть может быть немного шире. Глаза расположены по бокам от нее. Для дальнейшего вычисления пропорций лучше всего указать, где будут располагаться зрачки.
Чтобы определить, насколько высоко над глазами должны быть брови нужно разделить круг на четыре равные части, снизу вверх. По горизонтальной линии, проходящей прямо над глазами, будут располагаться брови.
Нос и губы
Вертикальную линию нижней части лица нужно разделить пополам. Отметка середины там, где должно быть основание носа. Ширину носа легко определить, проведя параллельные линии вниз от внутренних уголков глаз.
Оставшуюся часть — от носа до подбородка — нужно снова разделить пополам. Средняя линия совпадает с линией рта, то есть прямо над ней располагается верхняя губа, а под ней – нижняя. Ширину рта можно вычислить, проведя параллельные линии вниз от середины зрачков. Ширина подбородка обычно равна ширине носа.
Построение пропорций человеческого лица, описанное выше, является упрощенным методом и подходит для идеальных лиц, которых в природе не так много.
www.syl.ru
Пропорции при рисовании — Копилка знаний
Кубы.
Для развития навыков определения пропорций предметов расположите на столе несколько обыкновенных картонных коробок. Способом визирования, т. е. с помощью карандаша и большого пальца, определите размеры всех коробок. Коробка слева — это куб; у каждой ее грани высота и ширина одинаковы. У коробки, стоящей вертикально, высота относится к ширине приблизительно как три к одному. Определите сами размеры горизонтально лежащей коробки.

Рисуем кубы
Фрукты.
Когда вы рисуете округлые формы, такие как яблоко, груша и банан, вы также можете прибегнуть к помощи коробок. Представьте, какой тип коробки соответствует каждой из форм. Можно даже изобразить коробки. Подобно цилиндрическим телам, изогнутые формы этих фруктов вполне удобно разместятся в нарисованных выше коробках.
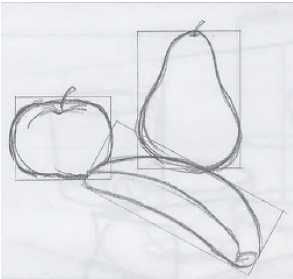
Рисуем фрукты
Бутыли.
Когда вы смотрите на цилиндрический предмет, подумайте, в какого типа коробку его можно поместить. Пропорции этих цилиндрических форм удивительно напоминают пропорции коробок на предыдущем рисунке. Чтобы изобразить эти предметы, вы можете начать с коробок, а затем нарисовать цилиндры внутри них.
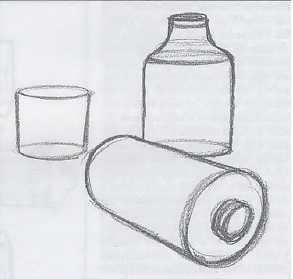
Рисуем бутыли
Деревья и кусты.
С помощью тех же коробок вы можете определить пропорции неправильных, сложных форм, таких как куст, ствол сломанного дерева и каменная глыба. Куст слева вмещается в коробку, которая имеет форму куба; дерево — в коробку, у которой высота относится к ширине приблизительно как два к одному. А наклонная каменная глыба помещается в коробке, имеющей длину, в два с половиной раза превосходящую высоту.

Рисуем деревья и кусты
По этой теме читайте на сайте :
kopilca.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Арифметика
Пропорции, члены пропорции. Основное свойство пропорции
Частное от деления числа a на число b называют отношением числа a к числу b.
Число a называют предыдущим членом отношения, число b – последующим членом отношения.
Пропорцией называют равенство двух отношений:
.
Иногда пропорцию записывают так:
a : b = c : d .
И в одной, и во второй формах записи пропорции числа a и d называют крайними членами пропорции, а числа b и c – средними членами пропорции.
Для любой пропорции справедливо следующее равенство, которое называют основным свойством пропорции:
Словесно это равенство можно сформулировать так: произведение крайних членов пропорции равно произведению средних членов пропорции.
Для того, чтобы доказать основное свойство пропорции, умножим пропорцию на выражение .
В результате получим:
что и требовалось доказать.
Основное свойство пропорции позволяет по трем любым известным членам пропорции найти четвертый неизвестный член пропорции. Покажем это на двух примерах.
Пример 1. Найти неизвестный член пропорции x , если
Решение. Воспользовавшись основным свойством пропорции, получаем:
Ответ: 3,15 .
Пример 2. Найти неизвестный член пропорции x , если
Решение. Воспользовавшись основным свойством пропорции, получаем:
Ответ: .
Из основного свойства пропорции легко вытекают также свойства пропорции, которые называют перестановкой членов пропорции. Эти свойства формулируются так: если
.
то
Производные пропорции
Справедливы также свойства пропорции, которые называют производными пропорциями. Эти свойства формулируются так: если
,
то
В качестве примера докажем первое из указанных свойств (остальные свойства доказываются аналогично). Для этого к обеим частям пропорции
.
достаточно прибавить 1. В результате получаем,

что и требовалось.
Замечание. Последнее из свойств пропорций является наиболее общим и может быть доказано, например, с помощью основного свойства пропорции.
Свойства равных отношений
Если выполнено соотношение
то выполнено и соотношение
где
k1 , k2 , … kn
– произвольные числа, которые не могут все одновременно равняться нулю.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
